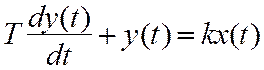Радиоавтоматика: основы теории и принципы построения автоматических систем, страница 16

,                                          (7.2)

где T – постоянная времени, обусловленная наличием емкости, индуктивности, момента инерции и т. д.; k – коэффициент передачи.

Передаточная функция инерционного звена

K(p) =k/(1+Tp).                                                 (7.3)

Амплитудно-частотная и фазо-частотная характеристики звена определяются выражениями:

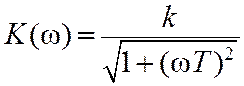,                                             (7.4)

.                                             (7.5)

Построенные по этим формулам АЧХ и ФЧХ инерционного звена для двух значений постоянной времени (T₂ > T₁) представлены на рис. 7.1.

Рис. 7.1

Чтобы построить ЛАХ звена, необходимо определить логарифмическую функцию АЧХ в децибелах из (7.4):

,

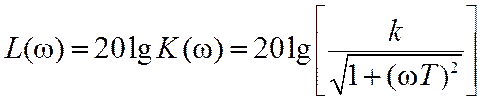или             

                    .                                (7.6)

Точное построение ЛАХ заключается в последовательном определении значений L(w) при различных частотах w. Построение ЛАХ обычно упрощают, заменяя точную L(w) ее асимптотами. Первая асимптота характеризует ЛАХ при малых частотах, когда величиной w²T² можно пренебречь, т. е. принимают

.                                            (7.7)

Эта асимптота не зависит от частоты. Вторая асимптота характеризует ЛАХ при больших частотах, когда w²T²>>1, т. е. принимают

.                                  (7.8)

Если принять приращение частоты на одну декаду (w₂ = 10w₁), то АЧХ в децибелах изменится на величину

.

Следовательно, для второй асимптоты известен наклон, характеризующий убывание амплитуды на 20 дБ при возрастание частоты на 1 декаду. Точка сопряжения обеих асимптот определяется равенством L¢(w) и L²(w), т. е.

,

откуда w_с=1/T.

Величина w_с определяется постоянной времени инерционного звена и называется сопрягающей частотой.

Асимптотическая ЛАХ, построенная по формулам (7.7), (7.8), представлена на рис. 7.2. Как видно из сравнения (7.6) с (7.7), (7.8), максимальное отклонение асимптотической ЛАХ от точной характеристики L_т(w) равно 3 дБ при частоте сопряжения w_c (эта частота определяет полосу пропускания по уровню 0,7) и незначительно при других частотах.

Рис. 7.2

Логарифмическая фазо-частотная характеристика инерционного звена

j(w)= –arctgwT= –arctg(w/w_c).

Для сопрягающей частоты фаза

j(w_c)= –arctg(w_c/w_c)= –arctg1= – p/4.

Переходная характеристика инерционного звена

,                                                  (7.9)

а импульсная

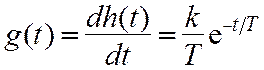.                               (7.10)

Построенные по формулам (7.9), (7.10) характеристики при двух значениях постоянной времени (T₂>T₁) представлены на рис. 7.3. Из рисунка видно, что время переходного процесса, определяемое как время установления значения

,

тем больше, чем больше постоянная времени (t_п@3T=3/w_c).

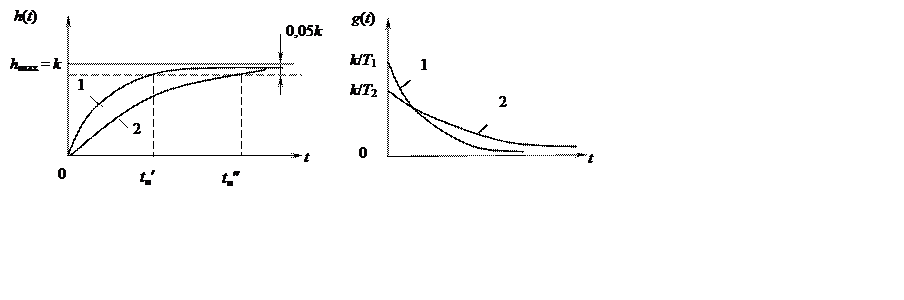
Рис. 7.3

Примерами инерционного звена являются: RC (или RL) фильтры нижних частот; дискриминатор (например, частотный); генератор постоянного (или переменного) тока; электродвигатель и т. д., если уравнения их динамики можно представить в виде (7.2).

7. 3. Интегрирующее звено

Уравнение динамики интегрирующего звена имеет вид

_или 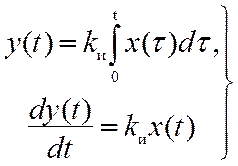                                                            ,                                (7.11)

где k_и – коэффициент передачи, имеющий размерность с ^–1.

          Передаточная функция интегрирующего звена

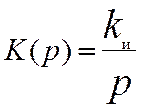,                                        (7.12)

а частотные характеристики определяются выражениями

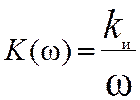,                                        (7.13)

j.                                   (7.14)

АЧХ и ФЧХ интегрирующего звена, построенные в соответствии с формулами (7.13) и (7.14), представлены на рис. 7.4.

 

Рис. 7.4

ЛАХ интегрирующего звена на основании (7.13) определяется как

L(w)=20lgK(w)=20lgk_и – 20lgw.                    (7.15)

Это выражение подобно (7.8), поэтому ЛАХ интегрирующего звена является прямой линией, проходящей с наклоном –20дБ/дек через точку на оси частот w=k_и.

 

Рис. 7.5

Логарифмическая фазо-частотная характеристика отличается от представленной на рис. 7.4 характеристики j(w) лишь масштабом по оси частот (логарифмический вместо линейного).

Переходная характеристика интегрирующего звена представляет собой линейную функцию времени, а импульсная – ступенчатую функцию     (рис. 7.5).

Примерами интегрирующего звена являются: интегратор на основе операционного усилителя, редуктор исполнительного устройства системы вращения антенны и др., если уравнения их динамики имеют вид (7.11).

ЛЕКЦИЯ 7. ТЕМА 7: «ТИПОВЫЕ ЗВЕНЬЯ СИСТЕМ

 РАДИОАВТОМАТИКИ»

(продолжение)

План лекции

Форсирующее звено.

Колебательное звено.

7. 4. Форсирующее звено

Динамические свойства форсирующего звена описываются уравнением

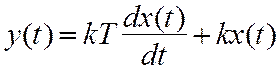,                                        (7.16)

где k – коэффициент передачи звена, Т – постоянная времени.

Передаточная функция форсирующего звена

К(р)=k(1+Тр).                                 (7.17)

АЧХ и ФЧХ звена на основании (7.17) определяются выражениями

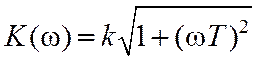,                                 (7.18)

j(w)=arctgwT.                                 (7.19)

Частотные характеристики форсирующего звена, построенные с использованием (7.18) и (7.19) для двух значений постоянной времени (Т₂>Т₁), представлены на рис. 7.6.

ЛАХ форсирующего звена получается из (7.18):

L(w)=20lgK(w)=20lg|k|,

или   

                                         L(w)=20lgk+20lg(1+w²T²)^1/2.                           (7.20)

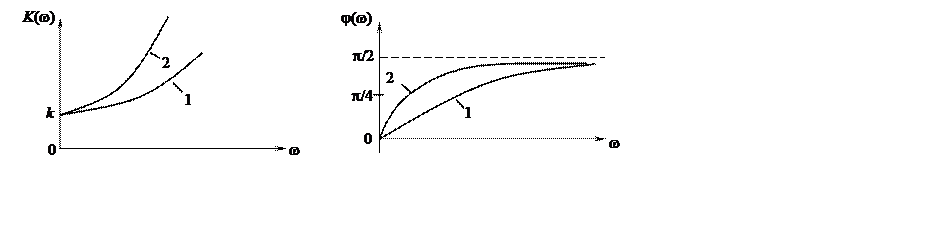
Рис. 7.6

Асимптотическая ЛАХ может быть представлена двумя прямыми:

L¢(w)=20lgk при w£ 1/T,

L²(w)=20lgk+20lgwT при w > 1/Т.                          (7.21)

Первая представляет собой отрезок горизонтальной прямой с ординатой 20lgk, а вторая – прямую, проходящую с наклоном 20 дБ/дек. Частота сопряжения w_с=1/Т этих прямых соответствует значениям АЧХ К(w_с)=k и ФЧХ j(w_с)=p/4. Максимальная погрешность аппроксимации ЛАХ составляет 3 дБ и соответствует частоте w_с.