На схеме (рис. 8.12) суммирующий узел заменён элементом сравнения, а коэффициент передачи дискриминатора взят с противоположным знаком. Это позволяет свести исходную схему (рис. 8.5) к схеме встречно-параллельного соединения звеньев (т. е. с отрицательной ОС). Звено с коэффициентом передачи, равным – 1, отображает элемент сравнения на входе системы (рис. 8.5) при условии, что воздействие отсутствует (х = 0).
В соответствии со схемой, представленной на рис. 8.12, искомая передаточная функция равна
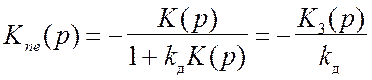 .
(8.7)
.
(8.7)
При совместном воздействии на систему и полезного сигнала и помехи анализ проводится раздельно для каждой составляющей (сигнальной и шумовой) с использованием соответствующих передаточных функций, а результаты (в силу принципа суперпозиции) складываются. Например, результирующая ошибка равна сумме динамической ошибки, обусловленной инерционностью системы по отношению к воздействию, и шумовой ошибки.
В ряде случаев необходимо знание передаточной функции
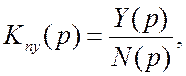
позволяющей определить характеристики помехи на выходе системы (такая задача возникает, например, при оценке спектральной чистоты выходного сигнала системы ФАПЧ). Эта передаточная функция может быть определена на основе структурной схемы (рис. 8.12), если полагать, что выходная переменная – это y, а цепь обратной связи имеет коэффициент передачи kд:
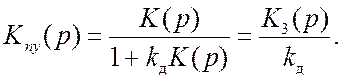 (8.8)
(8.8)
Приведенные выражения позволяют установить общее правило для нахождения передаточной функции замкнутой системы при любых точках приложения возмущения u (вход системы) и наблюдения реакции системы v (выход):
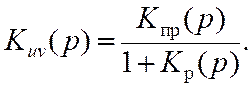
Здесь Кпр(р) – передаточная функция прямой цепи, т. е. разомкнутого участка цепи между точкой приложения воздействия и рассматриваемой выходной переменной; Кр (p) = kд K(p) – передаточная функция разомкнутой системы (при разомкнутой обратной связи).
В соответствии с результатами предыдущего пункта любая замкнутая система может быть представлена как линейный четырехполюсник с передаточной функцией Kз(p), устанавливающей связь между выходной yи входной x переменными (рис. 8.13).
Рис. 8.13
Такое представление следящей системы является условным, так как в реальных системах отсутствует вход, на который подавалось бы воздействие x (как и выход, соответствующий переменной y). Входом следящей системы является вход дискриминатора, на который подается сигнал (напряжение), зависящий от параметра х. Выходная переменная следящей системы – это, как правило, также напряжение (зависящее от параметра у). Однако представление системы в виде четырехполюсника удобно с точки зрения ее математического описания. Оно позволяет не только проводить анализ системы, но и пояснить такое важное ее свойство, как фильтрующая способность.
Действительно, передаточной функции Kз(p) соответствует комплексный коэффициент передачи (АФХ) Kз(jw), получаемый заменой переменной pна jw. Модуль АФХ есть амплитудно-частотная характеристика jз(w), а аргумент – фазо-частотная jз(w) характеристика замкнутой системы.
АЧХ замкнутой системы может быть получена экспериментально, если на вход подать сигнал заданной формы, параметр х которого изменяется по гармоническому закону:
![]() ,
,
где Хm– «амплитуда», имеющая определенный смысл для каждого типа систем (девиация частоты для системы АПЧ, индекс фазовой модуляции для системы ФАПЧ и т.д.). Под АЧХ замкнутой системы понимается зависимость от частоты отношения «амплитуды» Ym выходной переменной (также девиация, индекс фазовой модуляции и пр.) к «амплитуде» Xm входной переменной.
При значениях w, близких к нулю, система практически безошибочно отслеживает параметр x, т. е. Ym=Xm (точное равенство имеет место в астатических системах, которые преимущественно и используется). По мере увеличения w начинает проявляться инерционность системы, обусловленная конечной полосой пропускания: отношение Ym/Xm<1, стремясь в пределе при w®µ к нулю. Сказанное свидетельствует о том, что следящая система представляет собой фильтр нижних частот по отношению к воздействию x(t).
Типичный вид АЧХ замкнутой системы иллюстрируется рис. 8.14, а (кривая 1 соответствует системе с монотонной переходной характеристикой, а кривая 2 – системе с колебательной ПХ).
Конечная полоса пропускания системы приводит к специфической ошибке, называемой динамической ошибкой. Физический смысл возникновения этой ошибки поясняется рис. 8.14, б, на котором представлены АЧХ замкнутой системы (кривая 1) с полосой пропускания Dw0,7 (на уровне 0,7) и энергетический спектр воздействия Sx(w) (нормированный по значению Sx(0)). Как видно из рисунка, замкнутая система подавляет спектральные составляющие воздействия на частотах w >Dw0,7 (заштрихованная область под кривой 2),что и приводит к динамической ошибке (чем больше отличие Kз(w) от единицы, тем больше ошибка). Увеличение полосы пропускания системы позволяет уменьшить динамическую ошибку, однако полностью устранить ее невозможно. Объясняется это тем, что с увеличением Dw0,7 возрастает мешающее влияние шумов (имеющих более широкий спектр, чем воздействие). Выбор оптимальной полосы пропускания, позволяющей минимизировать суммарную ошибку (динамическую и шумовую), является важнейшей задачей проектирования радиотехнических следящих систем.
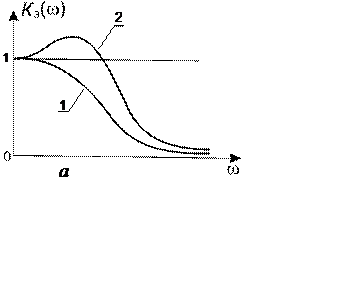
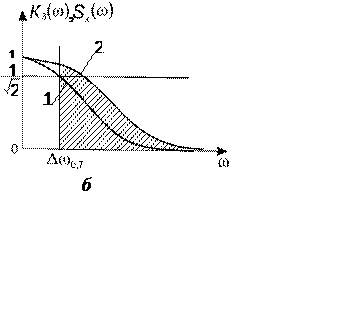
Рис. 8.14
Контрольные вопросы
1. Какой вид имеет обобщенная функциональная схема следящей системы? Укажите назначение ее элементов.
2. Что называется дискриминационной характеристикой? Чем определяется ее форма?
3. Что называется флуктуационной характеристикой дискриминатора? Какой вид она имеет?
4. Изобразите обобщенную структурную схему следящей системы? Напишите дифференциальное уравнение, ее описывающее.
5. Какой вид имеет обобщенная структурная схема линейной следящей системы? При каких условиях она применима?
6. Назовите основные способы соединения звеньев. Как при этом определяется передаточная функция эквивалентного звена?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.