По виду действующих в системе сигналов автоматические системы подразделяются на непрерывные и дискретные. В первом случае сигналы – непрерывные функции времени, во втором – дискретные (ступенчатые, импульсные). В свою очередь дискретные системы делят на импульсные и цифровые. Помимо временной дискретизации в цифровых системах осуществляется дискретизация (квантование) сигналов по уровню. При определенных условиях (когда полоса пропускания системы существенно меньше частоты дискретизации) дискретная система может быть заменена квазинепрерывной моделью, что позволяет проводить анализ таких систем известными методами (операторным, частотным или временным методами).
По виду уравнений, описывающих систему, все автоматические системы подразделяются на линейные и нелинейные. В первом случае они описываются линейными дифференциальными (или разностными для дискретных систем) уравнениями, во втором – нелинейными.
Система является линейной, если все ее элементы линейны. Звено является линейным, если его характеристика имеет вид y = kx, где k – коэффициент передачи, имеющий размерность [k] = [y]/[x]. Например, для усилителя k – безразмерная величина, для частотного или фазового дискриминатора соответственно В/Гц и В/рад, для электродвигателя – (рад/с)/В.
Строго линейных звеньев не существует. Даже для усилителя, который принято считать линейным звеном, амплитудная характеристика может полагаться линейной лишь в ограниченном диапазоне амплитуд входного сигнала. Однако на практике в целях упрощения анализа систем широко используют линейную аппроксимацию характеристик нелинейных элементов y = ƒ(x) (это относится в первую очередь к дискриминаторам).
Алгебраическое уравнение y=ƒ(x), описывающее связь между мгновенными значениями сигналов на входе и выходе звена в один и тот же момент времени, называют статической характеристикой. Она является исчерпывающей характеристикой для описания безынерционных звеньев, имеющих равномерную в полосе частот от нуля до бесконечности амплитудно-частотную характеристику (АЧХ). Реальные звенья являются инерционными, так как имеют конечную полосу пропускания. Для их описания используются динамические характеристики (дифференциальные уравнения или передаточные функции). В качестве примера можно привести распространенное звено – RC-фильтр нижних частот (ФНЧ), описываемый дифференциальным уравнением
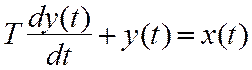, (1.1)
или передаточной функцией
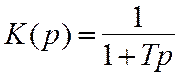, (1.2)
где T=RC – постоянная времени, имеющая размерность секунды.
При постоянном воздействии в установившемся режиме уравнение (1.1) принимает вид y(t)=x(t),что соответствует передаточной функции (1.2) K(p)=const=1. В переходном же режиме для описания ФНЧ необходимо использовать динамические характеристики (1.1) или (1.2). Если воздействие меняется во времени, то описание инерционного звена с помощью статической характеристики невозможно даже в установившемся режиме.
При анализе систем широко используют аппроксимацию характеристик различных функциональных элементов (усилителей, дискриминаторов и других), заменяя их безынерционными звеньями. Такая замена справедлива, если последовательно с элементом включен другой элемент со значительно более узкой полосой. Например, включение ФНЧ после дискриминатора часто позволяет считать предшествующий тракт приемника широкополосным, то есть заменить его безынерционным элементом.
По стабильности параметров системы во времени (постоянные или переменные параметры) все системы подразделяются на стационарные и нестационарные. Первые описываются уравнениями (дифференциальными или разностными) с постоянными коэффициентами. Примером нестационарной системы является система АРУ, содержащая нестационарный элемент (усилитель или аттенюатор с регулируемым во времени коэффициентом передачи).
По виду управляемой переменной системы подразделяются на системы АРУ, системы слежения за частотой (системы АПЧ), фазой (системы ФАПЧ), задержкой (ССЗ), направлением (ССН) и другие.
По виду используемой для управления энергии системы делят на электромеханические, электронные и прочие.
По числу управляемых переменных системы классифицируются на одномерные и многомерные.
Классификация реальных автоматических систем производится, как правило, по нескольким признакам одновременно. Например, цифровая система ФАПЧ (система нелинейна, так как содержит АЦП; дискретна из-за наличия устройства, осуществляющего временную дискретизацию, и предназначена для управления фазой (частотой) подстраиваемого генератора).
Контрольные вопросы
1. Укажите области применения типовых САУ.
2. Поясните сущность задач анализа и синтеза САУ.
3. Каковы задачи автоматического регулирования и управления?
4. Назовите основные функциональные элементы и нарисуйте функциональную схему замкнутой САУ.
5. В чем заключается сущность задачи управления и как она решается?
6. В чем заключается различие САУ, работающих по рассогласованию и по возмущению?
7.Проведите классификацию САУ и назовите основные признаки классификации.
ЛЕКЦИЯ 2
1.2. Системы автоматической регулировки усиления
Системы автоматической регулировки усиления (АРУ), их назначение и область применения.
Функциональная и структурная схемы системы АРУ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.