3. Какова структура «астатического» фильтра для системы второго порядка астатизма?
ТЕМА 14: «ОПТИМИЗАЦИЯ ПАРАМЕТРОВ РАДИОТЕХНИЧЕСКОЙ
СЛЕДЯЩЕЙ СИСТЕМЫ»
Задача оптимизации следящей системы при заданной структуре (известен вид передаточной функции) сводится к нахождению такой совокупности параметров системы (коэффициенты передачи, постоянные времени и пр. ), которая обеспечивает наилучшее (в смысле выбранного критерия) качество ее работы.
В зависимости от характера воздействия (детерминированное или случайное) в качестве критерия оптимальности системы используется условие минимума среднего квадрата (12.1), либо дисперсии (12.2) результирующей ошибки слежения.
Математическая формулировка задачи параметрической оптимизации сводится к нахождению экстремума (минимума) функции многих переменных (с1, с2, …, сn). Оптимальные значения параметров сiопт находятся как решение систем уравнений
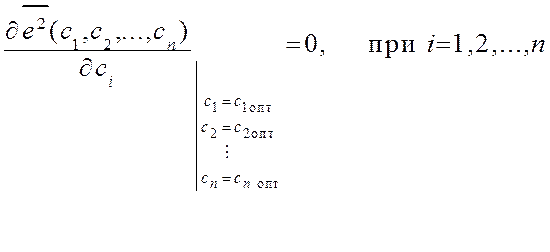 (14.1)
(14.1)
или
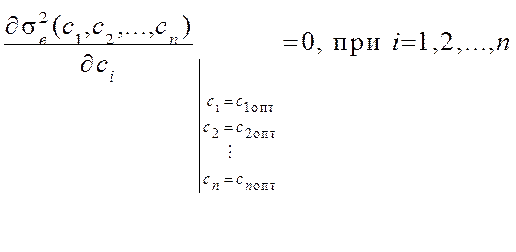 (14.2)
(14.2)
при некоторых ограничениях (дифференцируемость функции, единственность экстремума и др.).
Подстановка значений сiопт
параметров в соответствующие выражения для шумовой полосы системы и среднего
квадрата (или дисперсии) результирующей ошибки позволяет найти Fшопт и минимально
достижимую ошибку (т. е. ![]() или
или ![]() мин).
мин).
Рассмотрим пример параметрической
оптимизации автоматической системы (рис. 14.1) по параметру kи при воздействии ![]() и помехе
и помехе ![]() – белом шуме с спектральной плотностью
N0 Bт /Гц.
– белом шуме с спектральной плотностью
N0 Bт /Гц.
Оптимизацию проводим в соответствии с критерием (12.1), так как воздействие детерминированное.
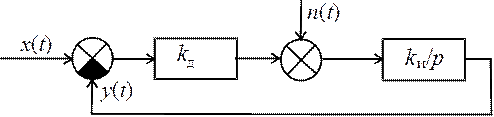
Рис. 14.1
Используя результаты лекций 12, 13, для среднего квадрата ошибки (12.1) запишем
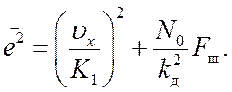 (14.3)
(14.3)
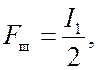
где
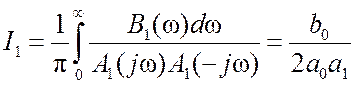 (14.4)
(14.4)
– табличный интеграл вида (12.9), а полиномы
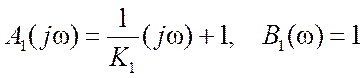
соответствуют передаточной функции замкнутой системы Kз(p)=1/[1+p(1/K1)].
Подставив значения параметров a0=1/K1, a1=1 и b0=1 в (14.4), находим I1=K1/2.
![]() (14.5)
(14.5)
Критерий оптимизации (14.1) в данном случае принимает вид
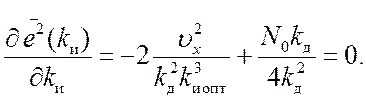 (14.6)
(14.6)
Решая уравнение (14.6), получаем
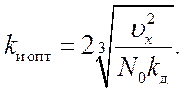
Оптимальное значение шумовой полосы и минимально достижимую ошибку
находим подстановкой ![]() в выражение для Fш (14.5) и
в выражение для Fш (14.5) и ![]() , (12.1):
, (12.1):
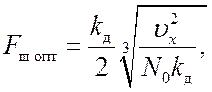 (14.7)
(14.7)
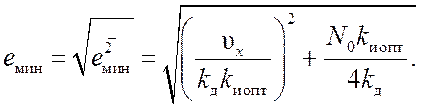
Анализ выражения (14.7) показывает, что оптимальное значение полосы
системы определяется скоростью изменения воздействия ![]() и
интенсивностью шума N0
(уменьшается с ростом N0).
и
интенсивностью шума N0
(уменьшается с ростом N0).
Контрольные вопросы
1. Сформулируйте критерий оптимизации следящей системы при детерминированном и случайном воздействиях.
2. В чём суть параметрической оптимизации замкнутой САУ?
3. Как объяснить существование оптимальной шумовой полосы системы?
ЛЕКЦИЯ 15. ТЕМА 15: «АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ
РАДИОАВТОМАТИКИ»
Нелинейные режимы работы САУ.
Основные методы анализа нелинейных САУ.
Графоаналитический метод анализа нелинейной системы АПЧ.
Определение полосы захвата и полосы удержания системы АПЧ графическим методом.
Нелинейной автоматической системой называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением (см. лекцию1).
Анализ нелинейных систем РА связан с преодолением значительных математических трудностей, так как не существует единого точного метода решения нелинейных уравнений. Разработанные методы позволяют решать лишь частные задачи, связанные с анализом нелинейных АС. К числу таких методов относятся: метод фазовой плоскости, метод кусочно-линейной аппроксимации, метод гармонической линеаризации, метод статистической линеаризации, метод моделирования и др. Дадим краткую характеристику указанных методов.
Метод фазовой плоскости применяется для анализа нелинейных систем,
описываемых уравнением порядка n≤2. На плоскости с координатами x и ![]()
![]() (
(
![]() =dx(t)/dt)
строится траектория движения системы. Плоскость и траекторию называют фазовыми.
Чаще всего x и x определяют ошибку
=dx(t)/dt)
строится траектория движения системы. Плоскость и траекторию называют фазовыми.
Чаще всего x и x определяют ошибку ![]() и
ее производную ė (например, для системы ФАПЧ – это фазовая и частотная ошибки
соответственно). По виду фазовой траектории оценивается качество работы АС.
и
ее производную ė (например, для системы ФАПЧ – это фазовая и частотная ошибки
соответственно). По виду фазовой траектории оценивается качество работы АС.
Метод кусочно-линейной аппроксимации используется в тех случаях, когда нелинейное звено ( например, дискриминатор) может полагаться безынерционным (см. лекцию1), а его характеристика (статическая) может быть аппроксимирована прямыми линиями на отдельных участках. В частном случае, когда прямолинейный участок один, имеем линейную систему (методы анализа линейных систем вам уже известны). На каждом линейном участке система может быть описана линейным дифференциальным уравнением и, следовательно, исследована известными методами. В точках «сопряжения» линейных участков решения «сшиваются»: значения переменных, соответствующие концу одного участка принимаются за начальные условия для последующего участка. Таким образом удается построить фазовую траекторию движения системы. Область применения данного метода ограничивается задачами, в которых число аппроксимированных участков нелинейной характеристики невелико (не превышает трех), а порядок дифференциального уравнения n≤2.
Метод гармонической линеаризациибазируется на замене нелинейного звена линейным звеном с параметрами, которые определяются из условия их «эквивалентности» при гармоническом сигнале: равенство амплитуд первой гармоники сигнала. Данный метод применим в том случае, когда следящая система содержит ФНЧ, включенный на выходе дискриминатора и отфильтровывающий все гармоники входного сигнала, кроме первой.
Метод статистической линеаризации основан на замене нелинейного звена линейным звеном с эквивалентными статистическими характеристиками выходного сигнала: математическим ожиданием и дисперсией. В случае нелинейного дискриминатора это означает равенство дискриминационной и флуктуационной характеристик нелинейного элемента (см. лекцию10) и его статистического эквивалента – безынерционного звена с коэффициентом передачи kд и сумматора, подключенного к выходу безынерционного звена. При этом нелинейность звена учитывается через зависимость коэффициента передачи kд (крутизны ДХ) от уровня входного сигнала и отношения сигнал/шум, а также через зависимость дисперсии σд2 флуктуаций на выходе дискриминатора от указанных параметров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.