Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 9

Розглянемо приклад.

Необхідно в довільній плоскій стержневій системі, що навантажена заданими силовими факторами визначити узагальнене переміщення довільної точки в напрямку i-j, тобто–?

– повне переміщення (т.т) по напрямку (i-j) від дії всіх зовнішніх силових факторів, що прикладені до даної пружної системи.

Застосовуючи принцип можливих переміщень для допоміжного стану і використовуючи як можливі переміщення дійсні для заданої силової системи, будемо мати інтеграл Мора для плоскої системи.

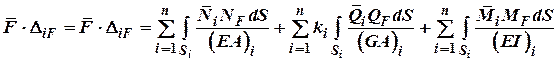
В загальному випадку дії сил на пружну систему інтеграл Мора буде мати такий вид:

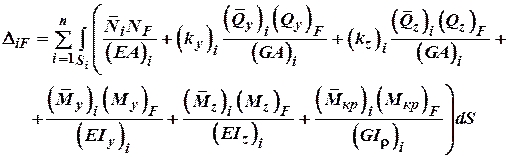
В більшості випадків при визначенні переміщень в брусах, рамах, фермах величиною поздовжньої деформації і деформаціями зсуву нехтують, а враховують лише переміщення, що виникають від дії згинаючих і крутних моментів. Тоді для плоскої системи переміщення через інтеграл Мора визначають так:

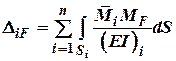
Для просторової пружної системи:

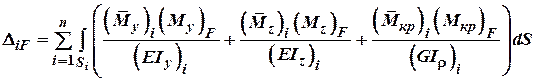
Для шарнірних ферм, що складаються із прямих стержнів, балок, рам будемо мати:

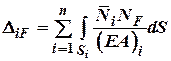
Для кінцевої довжини прямолінійних ділянок:

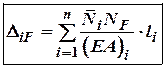– формула Максвела.

Правила розв'язання задач методом Мора

Для того, щоб визначити лінійне переміщення т.А в пружній системі за допомогою інтеграла Мора необхідно:

1. В силовій системі при необхідності визначити реакції від дії всіх зовнішніх сил;

2. Побудувати одиничну систему, навантаживши її при цьому одиничним навантаженням, в точці, переміщення якої необхідно визначити;

3. При необхідності визначаються реакції в одиничній системі;

4. Обидві системи розбити на ділянки;

5. Для кожної ділянки скласти закон змін згинаючих моментів від дії зовнішніх сил і одиничних сил;

6. Скласти інтеграл Мора і визначити його.

Якщо отриманий результат буде від'ємний, то знак "-" вказує на те, що переміщення заданої точки буде відбуватись в напрямку протилежному дії введеного нами одиничного навантаження.

При визначенні кутових переміщень увесь порядок розрахунків зберігається. Тільки замість одиничної системи в заданій точці прикладається одиничний момент.

Лекція №8

Визначення інтегралу Мора по методу Верещагіна.

Потенційна енергія деформації.

План лекції

1. Суть методу Верещагіна.

2. Порядок розрахунку задач по методу Верещагіна.

3. Приклади розрахунків.

4. Аналітичні залежності визначення потенційної енергії деформації (П.Е.Д.).

5. Визначення переміщення за допомогою П.Е.Д.

Література : [1] - ст. 373 - 379, [2] - ст. 400 - 405, 415 - 419.

Метод Верещагіна дозволяє графічно визначити інтеграл Мора і застосовується для визначення переміщень в прямолінійних системах, як плоских так і просторових.

Для криволінійних стержнів цей метод не прийнятний. Розглянемо це на конкретному прикладі.

Дано:

Визначити: -?

Розв'язок.

1. Оскільки ділянка брусу прямолінійна, то інтеграл Мора запишемо так:

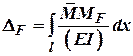
В нашому випадку він буде  виглядати так:

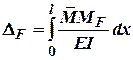
Позначимо площу силової епюри через, тоді на відстані від вільного кінця виділимо елементарну ділянку, площа якої буде визначатись так:

.

– це ордината на одиничній епюрі під центром ваги елементарної площадки, що була нами виділена.

т.С – центр ваги епюри.

Знаючи кут нахилу  одиничної епюри можна визначити величину згинаючого моменту в любій точці по довжині бруса, тобто

Відтак шуканий нами інтеграл Мора можемо записати так:

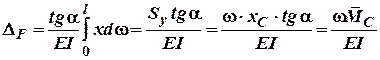
Таким чином інтеграл Мора дорівнює добутку площі епюри від дії зовнішнього навантаження на ординату прямолінійної епюри від дії одиничного навантаження, що знаходиться під центром ваги епюри від заданого зовнішнього навантаження.

А математично метод Верещагіна записується так:

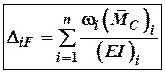
– площа епюри від дії зовнішніх силових факторів і розраховується для кожної ділянки окремо (кг-см²);

– ордината на одиничній епюрі під центром ваги вантажної епюри для кожної ділянки.

Якщо визначається кутове переміщення, то  – величина безрозмірна; при визначенні лінійного переміщення [] – см.