Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 12

Прикладом таких систем може служити стержнева підвіска, кронштейн, опорна колонка і ін.

В статично невизначних системах (СНС) кількість невідомих зусиль, що визначаться більша числа рівнянь рівноваги і, чим ця різниця вища, тим більше статично невизначною буде система.

Статична невизначеність системи позначається буквою, тобто буква  показує скільки "зайвих" зв'язків накладено на дану конструкцію.

Існує декілька методик розв'язання статично невизначених задач. Так один з шляхів розв'язку пов'язаний з розглядом чотириєдиної задачі:

1) Статична сторона – в якій складаються всі необхідні рівняння рівноваги.

2) Геометрична сторона – де оцінюються деформації системи. Рівняння, що оцінюють деформацію, називаються рівняннями сумісності деформацій, їх кількість завжди дорівнює степеню статичної невизначеності системи.

3) Фізична сторона – в якій встановлюється зв'язок між деформаціями і зовнішніми зусиллями чи деформаціями і напруженнями.

4) Синтез – тобто сумісний розв'язок трьох попередніх залежностей.

Приклад.

Дано:, , , ,.

Визначити: Напруження в перерізах колони

Розв'язок

1. Статична сторона задачі:

      (1)

2. Геометрична сторона задачі:                                                                 (2)

3. Фізична сторона задачі:

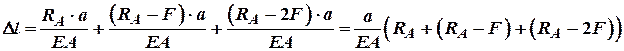.   (3)

4.Синтез.

Так як  і, а  то:

.

Підставивши це значення в (1) будемо мати; що; Таким чином:

;               ;               

Д.З.

Дано: мм²; мм²; мм²; мм²; МПа; кн.; мм.

Визначити:напруження на ділянках стержня

Рішення:

1. Встановити, чи буде задача статично визначною, чи ні.

2. Для цього необхідно:

2.1. Відкинувши нижню опору, визначити  для всього стержня і його знак

2.1.1. Якщо  – задача статично  визначна.

2.1.2. Якщо  –  задача статично невизначна.

Одним із найбільш загальних методів розв'язання є метод сил. Методика розрахунків має такі етапи:

1. Відкидаємо зайві зв'язки, чим перетворюємо саму систему в статично визначну так звану основну систему.

2.Замість відкинутих зв'язків прикладаємо невідомі зусилля позначаючи їх, , , …, , де  – ступінь статичної невизначеності. Отримана система носить назву еквівалентної.

3. Накладається умова еквівалентності заданої і перетвореної систем – відсутність переміщень в напрямку відкритих зв'язків. Ця умова і записується в канонічній формі методу сил.

Так, для  раз статично невизначних систем канонічні рівняння будуть мати такий вигляд:

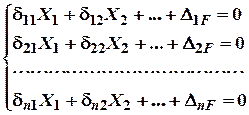
Всі коефіцієнти визначаються за допомогою інтеграла Макевела-Мора, що перетворені в кінцеву суму.

Силові коефіцієнти канонічних рівнянь визначаються так:

, де  –  внутрішня поздовжня сила від заданого навантаження;

– внутрішні зусилля від одиничного навантаження;

– довжина стержня.

Одиничні коефіцієнти з однаковими індексами визначаються так:

.

А з різними індексами так:                        .

Для визначення коефіцієнтів розглядають силовий і одиничний стан основної системи. Так для один раз статично невизначної системи канонічне рівняння має вигляд:                                               

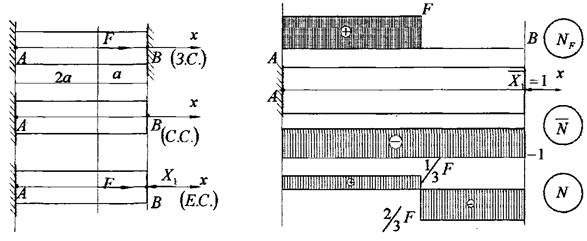
Розглянемо подібний попередньому, приклад 2.

Нехай дана система, що є один раз статично невизначеною. Оскільки із рівняння рівноваги визначається тільки одне невідоме зусилля.

Для розв'язання даної системи необхідно вибрати основну статично  визначну силову систему (С.С.), відкинувши правий зайвий зв'язок і залишивши його дію лінійною невідомою силою.

Відтак наша система буде еквівалентною системою (Е.С.). Для подальшого розв’язку на основну нашу систему в точці дії невідомого зусилля прикладемо т.з. одиничну силу. Побудуємо епюри поздовжніх внутрішніх зусиль окремо від дії зовнішнього заданого навантаження і вибраного нами одиничного зусилля .

Запишемо канонічне рівняння методу сил:.