Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 24

Деформації і напруження, що виникають при взаємному натиску одного тіла на друге, називають контактними. Як показують експериментальні дані матеріал, що не має можливості вільно деформуватись - перебуває в об'ємному напруженому стані, який досить швидко зменшується по мірі віддалення від точки контакту.

Вперше вирішення контактної задачі було запропоновано німецьким вченим Герцем (1881-1882). При розв'язанні задачі виходять із таких припущень:

1. Навантаження здійснюють в зоні контакту тільки пружні деформації, що слідують закону Гука;

2. Площадка контакту дуже мала в порівнянні з поверхнями тіл контакту;

3. Сили тиску, що розподіляються по поверхням контакту – нормальні до цих поверхонь.

І. Стиск (шарів) двох куль.

При стиску силами  двох куль з радіусами  і  утворюється кругла площадка контакту, радіус якої визначається по формулі:

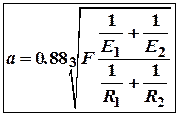, де,  – модулі пружності матеріалів куль.

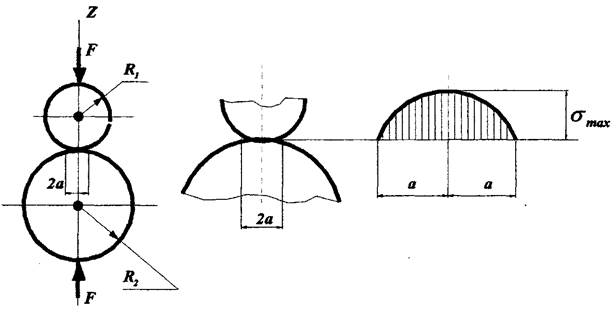
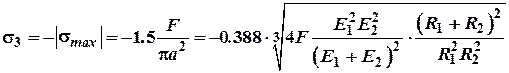
Два інших головних напруження в центрі площадки контакту будуть дорівнювати:

.

Таким чином в найбільш напруженій точці контакту матеріал знаходиться практично в умовах всебічного стиску (об'ємний стиск). Для визначення  використовуємо IV-y теорію міцності:

.

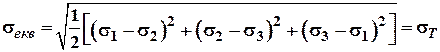Підставивши значення головних напружень будемо мати, що: в центрі площадки контакту.

Найбільше контактне дотичне напруження в загрозливій точці, що знаходиться на відстані  по напрямку осі  від площини контакту буде дорівнювати:

,

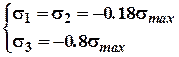
У випадку увігнутої поверхні одної із куль:

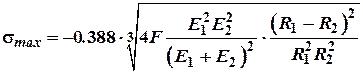
Якщо одна із поверхонь є площиною, тобто, то

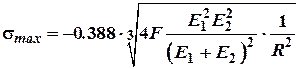
ІІ. Стиск циліндричних тіл.

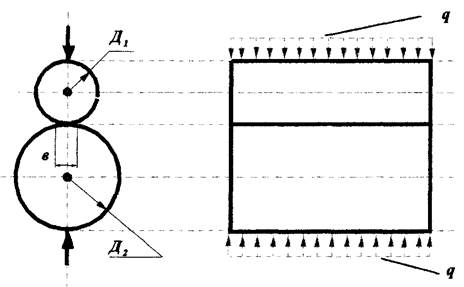
В цьому випадку зоною контакту буде вузька прямолінійна смужка, ширина якої визначається за формулою:

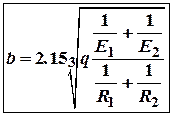
Найбільші напруження будуть вздовж смужки контакту.

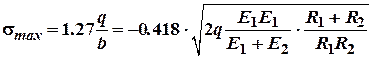
Найбільш небезпечна точка розміщується на глибині  по осі  і напруження, що діють в ній дорівнюють:

;     ;  ;  .

У випадку увігнутої циліндричної поверхні радіуса максимальні нормальні напруження будуть дорівнювати:

.

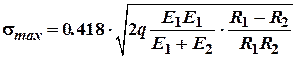При тиску циліндричної поверхні на площину:.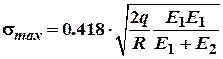

Ці формули отримані для, але вони справедливі і для любих коефіцієнтів Пуассона.

ІІІ. Загальний випадок контакту двох поверхонь.

В загальному випадку контакту двох тіл площадка контакту являє собою еліпс з напівосями:

;

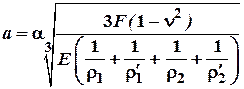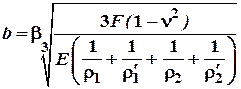, де  – коефіцієнт Пуассона; і  – радіуси кривизни в двох взаємно перпендикулярних напрямках одного із контактуючих тіл; і  – радіуси кривизни в двох взаємно перпендикулярних напрямках другого контактуючого тіла.

Коефіцієнти  і  табульовані і функціонально залежні від кута. Кут  – це кут між головними плоскостями кривизни тіл, що контактують:

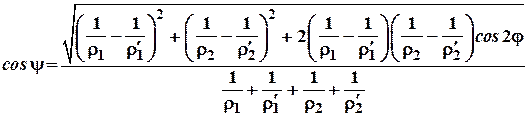
Максимальні напруження в цьому випадку:

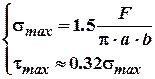
Із наведених формул видно, що контактні напруження залежать від пружних властивостей матеріалу і не мають лінійної функціональної залежності від навантаження. При зростанні навантаження зростання величина напружень уповільнюється так, як площадка контакту не залишається постійною, а починає збільшуватись.

Умова міцності при контактних напруженнях.

Враховуючи те, що в зоні контакту точки тіла знаходяться практично в об'ємному напуженому стані, то перевірку міцності необхідно проводити по ПІ чи IV теорії міцності:

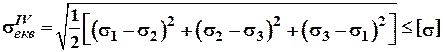
Виразивши головні напруження через  в центрі площадки контакту, умову міцності запишемо так:

 (*)

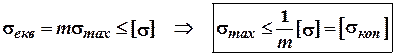де  – допустиме напруження для максимальних напружень у зоні контакту. Значення коефіцієнту  вибирається залежно від відношення  півосей еліпса площадки контакту із таблиць. Для цілого ряду конструктивних матеріалів табульовані і значення.

Порядок розрахунку на міцність елементів конструкцій при контактних навантаженнях.

1. Визначаються головні радіуси кривизни контактуючих тіл:, , , , а також;

2. Визначаються величини півосей еліптичної площадки контакту;

3. Визначаються найбільші напруження стиску в центрі площадки контакту.

4. Розрахунок на міцність ведуть за формулою (*). Як правило, виходячи при цьому із четвертої теорії міцності.