Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 6

При вирішенні задач по методу початкових параметрів необхідно:

1. Початок системи осей координат розмістити в крайній лівій точці балки, що розглядається;

2. Вираз для згинаючого моменту, складати, розраховуючи моменти сил, які розміщуються зліва від перерізу, що розглядається;

3. При включенні в рівняння зовнішнього моменту, його необхідно помножити на множник що дорівнює одиниці, де "" – абсциса точки, в якій діє цей зосереджений момент;

4. В тому випадку, коли розподілене навантаження закінчується раніше кінця балки, то його подовжують до кінця балки, а на довжину, подовженої таким чином дії розподіленого навантаження ділянки балки вводять "компенсуюче навантаження зворотного знаку".

5. Інтегрувати рівняння на всіх ділянках потрібно не розкриваючи при цьому дужок.

Розглянемо балку на двох опорах.

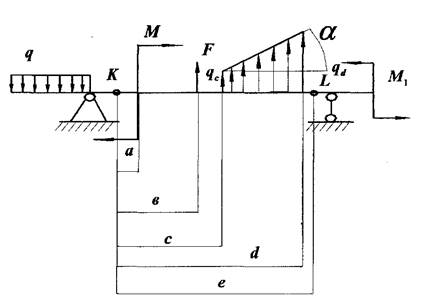
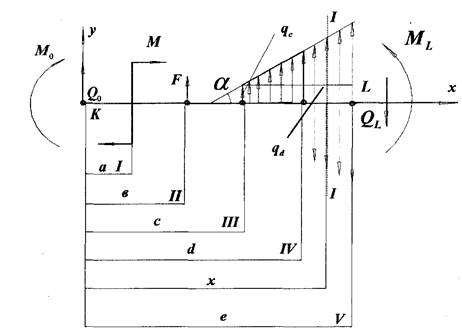
Будемо вважати, що  нам відомий, відтак. Запишемо вираз для згинаючого моменту в довільному перерізі X (V)-ї ділянки.

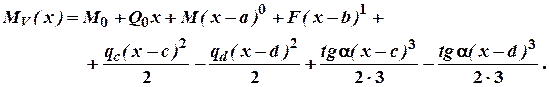
Тоді на ділянці IV вираз для моменту буде такий:

.

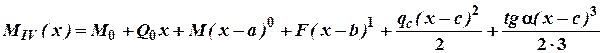Необхідно пам'ятати, що;  і т.д., завжди повинні бути більші нуля, тобто додатні. А згинаючий момент і поперечна сила, що співпадають з початком осей координат, отримали назву стичних початкових параметрів.

Маючи співвідношення для згинаючого моменту в довільній точці балки, запишемо для нього ДР пружної лінії на V і IV ділянках:

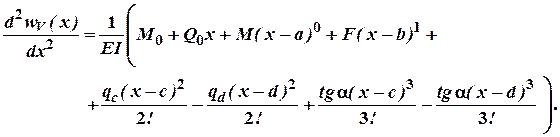
Проінтегрувавши обидві частини один раз-маємо:

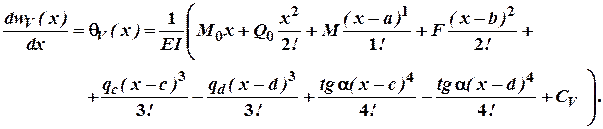
Інтегруючи другий раз не розкриваючи дужок будемо мати:

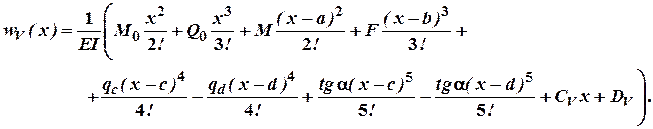
Аналогічно зробимо для четвертої ділянки:

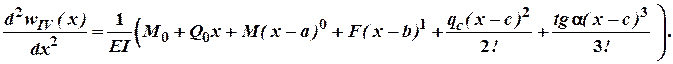
Проінтегрувавши двічі будемо мати:

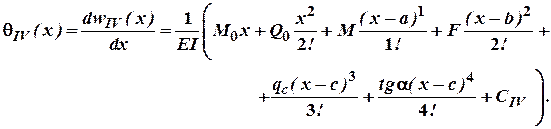
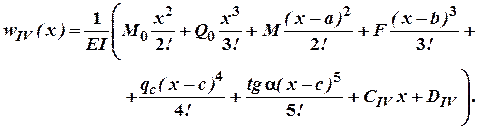
Враховуючи правило спряження ділянок і задавшись, що, тобто для кінця IV і початку V ділянок будемо мати, що, звідки. Точно так із двох інших рівнянь для і відповідно. Проводячи аналогічно для других ділянок будемо мати:

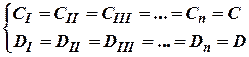
Величину цих констант  і  визначимо із рівнянь для кутів повороту і прогинів на початковій ділянці. Так для першої ділянки будемо мати:

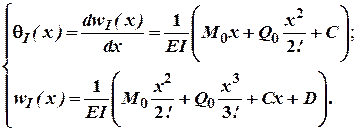
А при маємо:

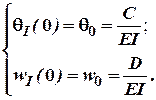
Таким чином довільні константи  і  дорівнюють відповідно куту повороту і прогину на початку відрахування, тобто в точці перетину осей координат. Прогин  і кут повороту отримали назву геометричні початкові параметри.

Підставимо тепер знайдені нами значення констант в рівняння для прогинів і кутів повороту в загальному випадку навантаження, будемо мати:

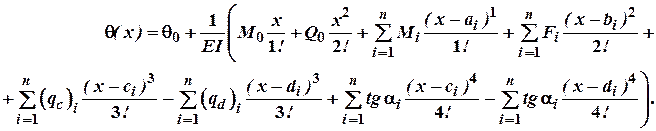
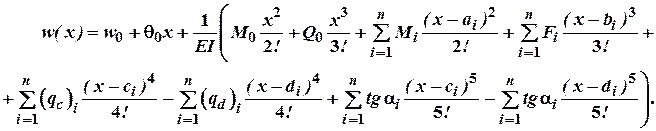
В отримані рівняння підставляють тільки ті навантаження, які знаходяться зліва від перерізу, що розглядається. Знаки доданків, що входять в рівняння, визначаються знаком відповідного силового фактору.

Таким чином, визначення переміщень по методу початкових параметрів зводиться в першу чергу до визначення величин початкових параметрів (, , ,). Статичні початкові параметри і знаходяться із умови рівноваги балки. А геометричні початкові параметри і визначаються із умов закріплення балки.

При вирішенні задач по цьому методу, початок системи осей координат, як вже відзначалось, розміщують в крайній лівій точці балки, що розглядається.

Лекція № 6

Загальні теореми для пружних систем.

Загальні методи визначення переміщень.

План лекції.

1. Узагальнені сили і узагальнені переміщення.

2. Робота зовнішніх сил.

3. Повні і одиничні переміщення в пружних системах.

4. Робота внутрішніх сил.

Література : [1] - ст. 353 - 361.

1. Узагальнені сили і узагальнені переміщення.

При оцінці деформації пружної системи під узагальненою силою  розуміють будь-яке зовнішнє навантаження, що діє на пружну систему.

Під узагальненим переміщенням  розуміють такий вид переміщення, на якому узагальнена сила здійснює роботу.

Так, для зосередженої сили узагальненим є будь-яке лінійне (поздовжнє) переміщення. Для зосередженого моменту узагальненим переміщенням може бути тільки кут повороту. Із теоретичної механіки робота постійної сили на переміщенні по напрямку її дії дорівнює добутку величини сили на вказаному переміщенні:

.

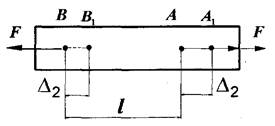
Під дією сил точки на брусі із положення по лінії дії сил, утворюючи відрізки  і. Відтак робота буде дорівнювати: