Сила, що відповідає даному
стану називається критичною, позначається (![]() ).
).
Критичною – називається сила, найменше перевищення якої приводить до втрати стійкого положення рівноваги тіла, чи конструкції.
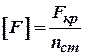 (1)
(1)
де ![]() –
допустиме навантаження при розрахунку на стійкість.
–
допустиме навантаження при розрахунку на стійкість.
![]() – коефіцієнт запасу стійкості.
– коефіцієнт запасу стійкості.
Для забезпечення запасу стійкості необхідно, щоб виконувалась основна умова:
![]() (2)
(2)
чи так: ![]()
Зруйнування конструкції від
втрати стійкості є одним із небезпечних видів руйнувань, адже відбувається при
напруженнях значно менших за![]() .
.
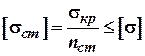 , (3)
, (3)
де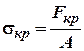 .
.
![]() – для пластичних
матеріалів;
– для пластичних
матеріалів;
![]() – для анізотропних
матеріалів (дерево і йому подібні);
– для анізотропних
матеріалів (дерево і йому подібні);
![]() – для крихких матеріалів
(чавун, скло).
– для крихких матеріалів
(чавун, скло).
Формула Ейлера для визначення
![]() при визначенні стійкості
при визначенні стійкості
стиснутих стержнів.
![]() Для
визначення
Для
визначення ![]() Ейлер домагався незначних
відхилень стержня від його початкового положення, при цьому
Ейлер домагався незначних
відхилень стержня від його початкового положення, при цьому ![]() (пропорційності)Через те, що деформації при
цьому були дуже малі, використовувалось ДР пружної лінії для балки:
(пропорційності)Через те, що деформації при
цьому були дуже малі, використовувалось ДР пружної лінії для балки:
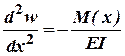 , (4)
, (4)
при цьому,для розрахунку приймається, що (ЕІ) мінімальна.
В правій частині ДР (4)
завжди буде знак "–" оскільки знак прогину і знак другої похідної від
нього, тобто моменту, що визвав цей прогин, будуть різні, при любому
(![]() ).
).
При 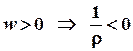 і навпаки,
і навпаки,
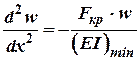 , (6)
, (6)
де![]() . Перепишемо (6) так:
. Перепишемо (6) так:
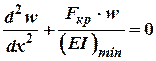
Позначимо: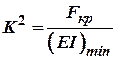 . Тоді:
. Тоді:
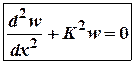 (7)
(7)
Розв'язком цього рівняння буде вираз:
![]() ,
,
1. При![]() :
: ![]() .
.
2. При![]() :
: ![]() , а так як
, а так як![]() , то
, то![]() .
.
Відповідно:![]() . Тоді:
. Тоді: 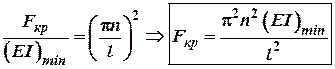 (8)
(8)
Ця формула вперше була
отримана для шарнірно закріпленого стержня. При визначенні максимального
прогину необхідно взяти першу похідну по ![]() від
-
від
-![]() , тобто визначити
екстремум функції прогину
, тобто визначити
екстремум функції прогину![]() .
.
Оскільки![]() , то
, то ![]()
![]() , то
, то
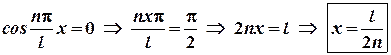 (9)
(9)
При ![]() тобто посередині стержня,
от же
тобто посередині стержня,
от же ![]() – це число напівхвиль,
що можуть бути розміщені по довжині стержня.
– це число напівхвиль,
що можуть бути розміщені по довжині стержня.
Поняття про приведену довжину стержня.
Коефіцієнт зведеної довжини.
Зведеноює така довжина стержня, на якій розміщується одна напівхвиля синусоїди.
![]() Довжини,що показано
пунктиром і є звееденими.
Довжини,що показано
пунктиром і є звееденими.
![]() (10)
(10)
де ![]() –
коефіцієнт зведення довжини. Відтак формула Ейлера при любих закріпленнях
стержня буде виглядати так:
–
коефіцієнт зведення довжини. Відтак формула Ейлера при любих закріпленнях
стержня буде виглядати так:
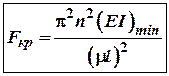 (11)
(11)
Поняття про критичні напруження.
Графік залежності від гнучкості.
Емпірічна формула Ясинського.
Критичне напруження ![]() – це напруження, що
виникає в стержні від дії на нього
– це напруження, що
виникає в стержні від дії на нього![]() .
.
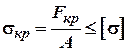 , де
, де ![]()
Як уже відомо, виведення
формули Ейлера базується на використанні ДР пружної лінії бруса. Так як область
її використання знаходиться не вище ![]()
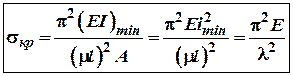 , (12), де
, (12), де 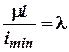 – гнучкість стержня.
– гнучкість стержня. ![]() – максимальна гнучкість
стержня.
– максимальна гнучкість
стержня.
Гнучкість - це відношення зведеної довжини стержня до радіусу еліпса його інерції.
Визначити загрозливу гнучкість стержня за даних умов закріплення
![]()
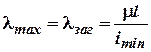 ;
;
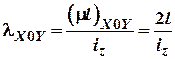 ;
;
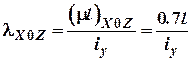 .
.
Залежно від розмірів прямокутного перерізу таке його розміщення буде найраціональнішим. Раціональною конструкцією є система, у якої гнучкість в усіх площинах буде однаковою.
Повертаючись до вище
сказаного, можемо констатувати, що формулою Ейлера можна користуватись тільки
до тих пір, доки діюче напруження стискання не перевищує![]() , тобто:
, тобто:
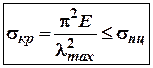 (12)
(12)
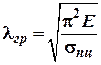 . (13)
. (13)
Із формули (13) витікає, що ![]() границя та
гранична гнучкість стержня починаючиз якої можна користуватись формулою Ейлера.
Таким чином, при
границя та
гранична гнучкість стержня починаючиз якої можна користуватись формулою Ейлера.
Таким чином, при![]() .
.
![]() –
для сталей
–
для сталей
![]() –
для чавунів
–
для чавунів
![]() –
для дерева
–
для дерева
Графік залежності критичних
напружень від гнучкості ![]()
Формула Ясинського ![]() (15)
(15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.