Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 23

Закон розподілу сил інерції є масовим (тобто ці сили діють на кожну одиницю маси), а значить і розподіл по перерізу буде таким, як показано на рисунку. В довільному перерізі  (із подібності трикутників).

Відтак величина потенційної енергії, що накопичена в стержні в довільному перерізі буде дорівнювати:

.

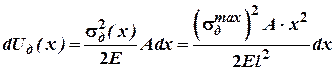Енергія, що накоплена в стержні дорівнює:

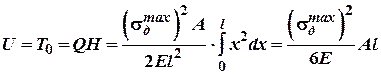
оскільки  то, а так як висоту, з якої падає тіло можна виразити через швидкість в момент удару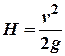, то:

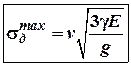
позначимо.

2. Напруження в стальному канаті при різкому гальмуванні.

Найбільш небезпечним є стан коли гальмування відбувається при опусканні, так як при цьому сила ваги і сила інерції сумуються.

В момент гальмування, на основі балансу енергії, для визначення динамічного подовження тросу маємо:

.

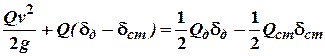Так як, то маємо:

.

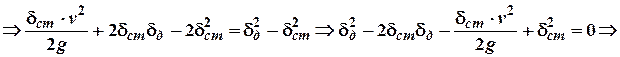
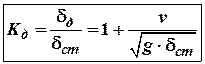– коефіцієнт динамічності при різкому гальмуванні. Звідси умова міцності при ударі:

.

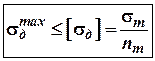, де

Урахування маси стержня, що зазнає повздовжнього удару.

При співударі тіла вагою і стержня, розглядається в процесі точного розрахунку необхідно враховувати те,  що процес удару має дві стадії:

1) На першій стадії в момент співудару  швидкість  тіла вагою, що набуло її до моменту співудару, падає до величини, за рахунок місцевих пластичних деформацій, що мають місце в перерізі, який сприймає удар;

2) Процес спільного руху тіла вагою  і стержня. Початкова швидкість для цього процесу буде дорівнювати швидкості. При точному розрахунку ми повинні враховувати зміну швидкості, а також ту кінетичну енергію, яку буде мати сам стержень, що деформується (при наближеному розрахунку ми враховуємо тільки його потенціальну енергію деформації).

Врахуємо швидкість довільного перерізу стержня:. Тоді кінетична енергія довільної ділянки маси стержня буде дорівнювати:

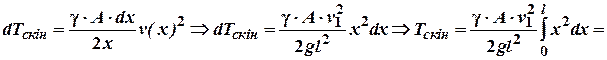
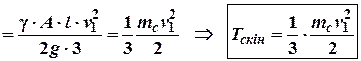
Таким чином, якщо в перший момент тіло, вагою, має кінетичну енергію, що дорівнює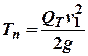, то втрата енергії за рахунок пластичних деформацій на початку другого етапу буде дорівнювати:

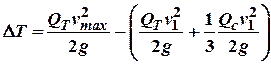, а із балансу енергії матимемо:

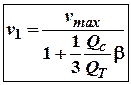
де  – швидкість вантажу і стержня на початку другого стану співудару.

Таким чином енергія удару (в системі тіла) на початку другого етапу удару буде становити:

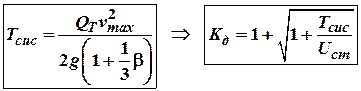, де  – кінетична енергія удару в системі тіло-стержень на початку другого етапу удару; – потенційна енергія деформації стержня.

Динамічний коефіцієнт, виражений через швидкість  в момент удару:

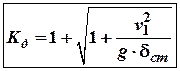
Відтак максимальні напруження в стержні, що сприймає удар будуть дорівнювати:

, (*)

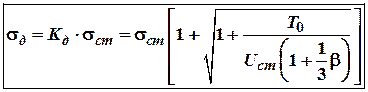де,.

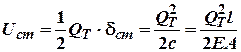чи так

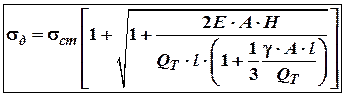
Самостійно:1. При скручуючому ударі. 603 - 604.

2. Розрахунок на удар при згині. 606 - 609

Механічні властивості матеріалів.

Для перевірки здатності матеріалу чинити опір дії ударних навантажень застосовують особливий вид випробувань - ударний згин, що дозволяє оцінити ударну в'язкість матеріалу.

Ударною в’язкістю матеріали(КС) називається величина роботи руйнування зразка, що віднесена до площі його поперечного перерізу.

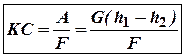
, (Дж/м²)

де  – висота підйому маятника копра перед випробуванням.

– висота вильоту маятника копра після руйнування зразка, що випробовувався;

– сила ваги копра.

Величина КС є оціночною характеристикою матеріалу і особливо враховується при виготовленні деталей, що працюють в умовах дії ударних навантажень, її величина суттєво залежить від температури в робочих умовах.

Різко знижується при зниженні температури практично для всіх матеріалів. Для вуглецевих сталей таким же критичним інтервалом є температура від (200-550)°С.

Лекція № 16

Контактні напруження. Формули для їх визначення. Умовиміцності

План лекції.

1. Основні поняття та припущення.

2. Стиск двох куль (шарів).

3. Стиск циліндричних тіл.

4. Загальний випадок контакту двох поверхонь.

5. Умова міцності при контактних навантаженнях.

6. Порядок розрахунку на міцність при контактних навантаженнях.

Література: [1] -ст. 613 - 617.