![]() (5)
(5)
де ![]() і
і
![]() – константи.
– константи.
Якщо задана початкова
координата тіла ![]() і швидкість
і швидкість ![]() при
при![]() , то враховуючи, що перша
похідна по часу від ординати
, то враховуючи, що перша
похідна по часу від ординати ![]() рівняння
(5) буде:
рівняння
(5) буде:
![]() , то ми можемо визначити постійні інтегрування:
, то ми можемо визначити постійні інтегрування:
![]() ,
а
,
а ![]()
Підставимо значення ![]() і
і ![]() в рівняння (5). Маємо:
в рівняння (5). Маємо:
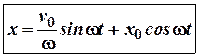 (6)
(6)
Позначимо![]() , а
, а ![]() і підставимо в рівняння
(6). Будемо мати:
і підставимо в рівняння
(6). Будемо мати:
![]() (7)
(7)
де ![]() –амплітуда вільних коливань;
–амплітуда вільних коливань; ![]() – фаза
коливань;
– фаза
коливань; ![]() – кут зсуву фази коливань.
– кут зсуву фази коливань.
При цьому:![]() , так як
, так як![]() ;
;![]() , то;
, то;
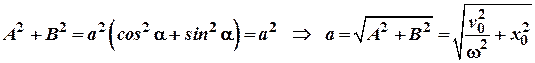
Відношення: 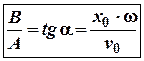
Нагадаємо, що під круговою
частотою (![]() ) мається на увазі число
коливань, що відбуваються на протязі
) мається на увазі число
коливань, що відбуваються на протязі ![]() секунд.
А знаючи власну (кругову) частоту легко можна визначити і період таких коливань
секунд.
А знаючи власну (кругову) частоту легко можна визначити і період таких коливань![]() , тобто час одного повного
коливання.
, тобто час одного повного
коливання.
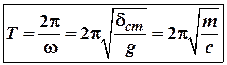 (8)
(8)
Величина, зворотна до періоду коливань визначає число коливань в одиницю часу і носить назву секундної частоти:
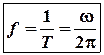 (9)
(9)
![]() (10)
(10)
Вимірюється в Герцах.
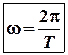 (11)
(11)
Розрахунки періоду і частоти коливань, виходячи із умов міцності і жорсткості.
![]() Прикладом
реальної системи коливань може служити система з одним ступенем вільності, яка
складається з тонкого пружного стержня з вантажем на кінці.
Прикладом
реальної системи коливань може служити система з одним ступенем вільності, яка
складається з тонкого пружного стержня з вантажем на кінці.
1. Виходячи з умови міцностіми можемо записати, що:![]() .
.
Враховуючи, що ![]() запишемо, що діюче на
стержень зусилля не повинно перевищувати:
запишемо, що діюче на
стержень зусилля не повинно перевищувати:![]() . А враховуючи жорсткість:
. А враховуючи жорсткість:
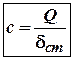 (2)
(2)
ми можемо записати, що 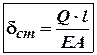 (3)
(3)
Відтак зусилля, що визначає
статичну деформацію![]() , буде визначати
необхідну жорсткість стержня:
, буде визначати
необхідну жорсткість стержня:
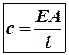 (4)
(4)
Тоді, власна (кругова}
частота коливань підвішеного тіла вагою ![]() буде
дорівнювати:
буде
дорівнювати: 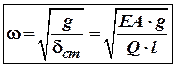 (5)
(5)
або ж так: 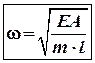 (5’)
(5’)
Відтак період коливань і
секундна частота коливань цього тіла будуть визначатись так: 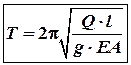 (6)
(6)
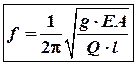 (7)
(7)
Із наведеного легко впевнитись, що власна частота коливань тіла буде тим вища, чим менше статичне подовження стержня.
2. Для балки жорстко защемленої
з тілом вагою ![]() на кінці
на кінці
![]() 2.1. Умова міцності:
2.1. Умова міцності:
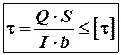 (1)
(1)
2.2. Власна (кругова) частота: 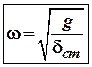 (2)
(2)
2.3. ![]() (максимальний
прогин).
(максимальний
прогин).
2.4.Максимальний прогин дорівнює: 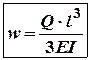 (3)
(3)
Підставимо (3) в (2) і, враховуючи,
що ![]() будемо мати:
будемо мати:
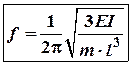 , а
, а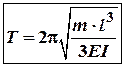 (4)
(4)
![]() –
секундна частота (вимірюється в герцах);
–
секундна частота (вимірюється в герцах); ![]() –
період коливань в секундах.
–
період коливань в секундах.
3. Для балки з тілом вагою![]() , що знаходиться
посередині:
, що знаходиться
посередині:
![]() 3.1. Виходячи з умов міцності
при згині
3.1. Виходячи з умов міцності
при згині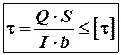 , знаходимо допустиму вагу
тіла для заданої балки.
, знаходимо допустиму вагу
тіла для заданої балки.
3.2. Максимальний прогин буде
дорівнювати статичній деформації:![]() .
.
3.3.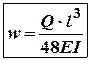 . Оскільки
. Оскільки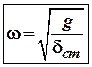 , то при
, то при ![]() будемо мати, що:
будемо мати, що:
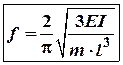 , а
, а 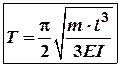
Самостійно:
1. Крутильні коливання
2. Вільні коливання системи з одною стелінню вільності з урахуванням опору, пропорційного швидкості (Писаренко ст. 525 - 526. ст. 531 - 533.)
Вимушені коливання пружних систем з одним ступенем вільності.
Якщо на тіло разом з
постійною силою тяжіння ![]() діє
періодична збуджуюча сила
діє
періодична збуджуюча сила![]() , то
ДР таких коливань системи можна записати в такому вигляді:
, то
ДР таких коливань системи можна записати в такому вигляді:
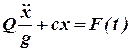 (1)
(1)
або 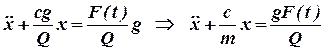 (2)
(2)
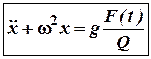 (3)
(3)
Розглянемо довільний випадок,
коли діюче зусилля ![]() буде
пропорційне
буде
пропорційне![]() . Позначимо
. Позначимо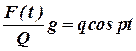 . При цьому період
коливань і частота коливань сили
. При цьому період
коливань і частота коливань сили ![]() будуть
визначатись так:
будуть
визначатись так: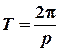 ;
;![]() . Відтак рівняння (3)
запишемо так:
. Відтак рівняння (3)
запишемо так: ![]() ,
(4)
,
(4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.