Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 15

Так при "" шарнірних опор вона буде рази статично невизначною. Число зайвих зв'язків, таким чином, буде дорівнювати числу проміжних опор.

При защемленні одного із кінців балки ступінь статичної невизначеності збільшується на одиницю і буде дорівнювати.

Для спрощення розв'язку такого роду задач в місцях зайвих опор ставлять шарніри, а зайвими невідомими в цьому випадку будуть згинаючі моменти в місцях їх розміщення.

Напрямок невідомих згинаючих моментів вибирається довільно (в нашому випадку - додатній)

При такому виборі для навантаження на інші прольоти балки передається тільки за допомогою невідомих моментів в шарнірах.

Складаючи додаткові рівняння переміщень для опорних перерізів можемо записати:

                          (1)

Так як основна система складається із двох опорних балок, що не зв'язані одна з одною, то можна розглянути два найближчі прольоти, наприклад, до -ої опори:

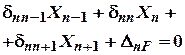       (2)

Для визначення переміщень "" і "", що входять в рівняння (2), побудуємо епюри згинаючих моментів в основній системі окремо від заданого навантаження і від кожного "зайвого невідомого", що дорівнює одиниці.

Використовуючи метод Верещагіна запишемо:

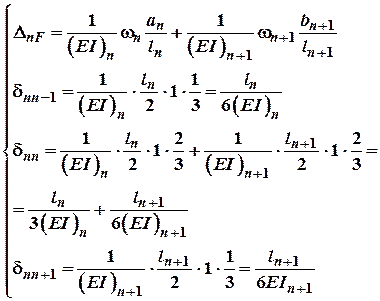                    (3)

Внесемо вираз (3) у вираз (2) будемо мати:

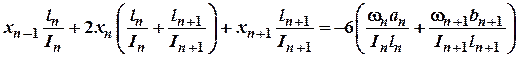           (4)

Оскільки зайвими невідомими у нас були згинаючі моменти. То замінивши їх на "", будемо мати рівняння, яке отримало назву трьох моментів:

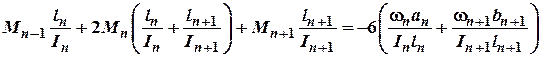       (5)

Таких рівнянь складається стільки, скільки вводиться шарнірів, що утворюють основну систему. В кожне із цих рівнянь трьох невідомих опорних моментів;;. Перше і останнє рівняння складаються із двох невідомих моментів. Його розв'язок проводиться методом послідовного виключення невідомих.

В тому випадку, коли  рівняння приймає вигляд:

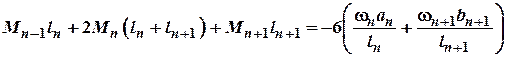              (6)

Приклад.

Якщо один із кінців балки має защемлення, то його або замінюють додатковим прольотом нескінченно малої довжини  тобто, або  ж даний прольот має нескінченно велику жорсткість тобто.

Для даного прикладу замінимо защемлення лівого кінця балки, додатковим прольотом, де. Відтак рівняння трьох моментів будуть мати такий вигляд:

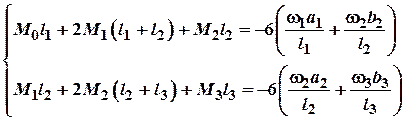
Так як, а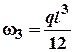;;;, то наша система рівнянь трьох моментів прийме такий вигляд:

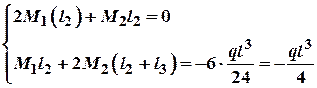
Визначивши із цієї системи опорні моменти, знаходимо реакції опор від заданого навантаження і від дії знайдених опорних моментів для кожної балочки окремо.

Так, позначивши ці реакції, наприклад, для третього прольоту через  і  запишемо:

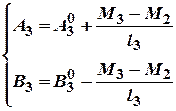
де  і  – реакції тільки від заданого навантаження на прольоті "З". Відтак повна реакція на прольоті "З" буде дорівнювати:

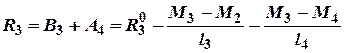
Тут   реакція опори "З" викликана дією заданого навантаження, що прикладене до прольотів  і.

Після визначення будують епюри і  для кожної двохопорної балки основної системи. Сумарну епюру (і) будують складаючи епюри від зовнішніх навантажень і знайдених опорних моментів по ділянках.

(Самостійно:розібрати приклад 68 ст.410-412)

Лекція 12

Стійкість стиснутих стержнів

План лекції:

1. Типи конструкційної стійкості стержнів

2. Формула Ейлера для визначення критичної сили

3. Поняття про критичні напруження. Емпіричні залежності Ясинського

4. Основні типи розрахунків стержнів на стійкість

Література : [1] - ст. 491 - 508. [2] - ст. 619 - 644.

Стійка конструкція - це конструкція, яка зберігає під дією зовнішнього навантаження свою початкову форму пружної рівноваги.

Розглянемо випадок стискання стержня поздовжнім зусиллям.

Існує три стани тіла в одному із яких воно може при цьому перебувати: - стійка рівновага – це коли при незначному відхиленні від стану рівноваги тіло намагається повернутися в своє початкове положення; – нестійка рівновага – коли тіло виведене з положення рівноваги зовнішнім зусиллям продовжує деформуватись в напрямку його дії, і в своє початкове положення не повертається; – байдужа, або критична рівновага – тіло при цьому стані знаходиться в початковій своїй формі, але навіть при  незначному зростанні діючого зовнішнього зусилля може її втратити.