Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 14

Із цього рівняння ми знаходимо невідоме зусилля в т.В: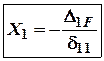      

Приклад 2.

Необхідно розкрити статичну невизначеність системи, що показана на малюнку, і побудувати для неї епюри  і.

Розв'язок.

1. Балка один раз С.Н.

2. Вибираємо основну статично визначну систему

3. Будуємо еквівалентну систему

4. Запишемо канонічне рівняння методу сил:

5. Навантажимо осн. сис. в т.В. одиничним навантаженням  в напрямку дії, вибраного нами.

6. Будуємо епюри згинаючих моментів від одиничної сили  і заданого навантаження, причому вантажну епюру розіб'ємо на дві, як показано на рис.

7. Визначимо переміщення від заданих сил:

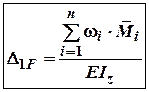
де      – площа епюри відповідного, для заданої ділянки, навантаження.

– ордината на одиничній епюрі під центром ваги ділянки площі вантажної епюри і позначається, частіше всього, через "". Відтак:

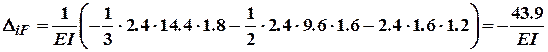
8. Визначимо переміщення від одиничної сили

9. Підставимо отримані вирази для  і  в вихідне канонічне рівняння і визначимо зусилля в т.В:

кН.

10. Оскільки ми отримали із знаком "+", то означає, що напрямок її дії вибрано вірно і тепер необхідно побудувати результуючі епюри і, як показано на рисунку.

Якщо система більш ніж один раз статично невизначна, то порядок розрахунків запишемо таким же, тільки збільшується число невідомих зусиль і відповідно кількість канонічних рівнянь для визначення переміщень. Приклад 2.

Так для балки, що показана на рисунку, необхідно:

1. Статично невизначна система 2р.

2. Вибираємо варіант статичної системи (осн. система)

3. Основну статично невизначну систему перетворюємо в еквівалентну.

4. Будуємо одиничні системи, тобто в точці визначення невідомих зусиль розміщуємо одиничні сили. Умовою еквівалентності, як уже відмічалось, є рівність деформацій  в заданій і еквівалентній системах.

Таким чином дані системи еквівалентні, якщо  і, тобто переміщення в точках 1 і 2 будуть дорівнювати нулю.

Відтак система канонічних рівнянь прийме такий вигляд:

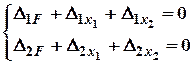
де      – переміщення точки 1 за рахунок дії зовнішніх сил;

– переміщення точки 2 за рахунок дії зовнішніх сил;

– переміщення точки 1 за рахунок дії сили по її ж напрямку дії;

– переміщення точки 2 за рахунок дії сили по її ж напрямку дії;

– переміщення точки 1 за рахунок дії сили  по її ж напрямку дії;

– переміщення точки 2 за рахунок дії сили по її ж напрямку дії.

Фізичний зміст отриманого нами канонічного рівняння полягає в тому, що сума переміщень точок системи за рахунок дії всіх зовнішніх і за рахунок всіх невідомих сил в точках їх прикладання повинно дорівнювати нулю.

Одиничні сили завжди співпадають по напрямку невідомими зусиллями, які розшукуються.

Любим відомим методом, – Мора чи Верещагіна, – визначають переміщення в точках 1 і 2, тобто отримуємо  і. Для визначення другої групи невідомих переміщень необхідно записати, що:

;    ;    ;   

і  – основні питомі переміщення. Вони завжди більші нуля, оскільки отримуємо їх за рахунок перемножування одиничних епюр самих на себе, тобто і площу і ординату беремо з одної і тої ж епюри.

– можливі питомі переміщення, які можуть бути як  так і, але вони завжди рівні по величині і по знаку. Відтак:

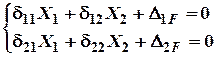
Це є канонічне рівняння методу сил для два рази статично невизначної системи. Для нескінченого числа  статично  невизначних  пружних систем канонічне рівняння методу сил буде мати такий вигляд:

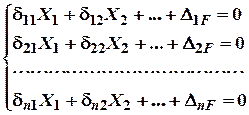
Лекція 11

Багатопрольотні нерозрізні балки. Рівняння трьох моментів.

План лекції:

1. Основні особливості і поняття методу.

2. Приклади розрахунків.

Література : [1] - ст. 405 - 414

Нерозрізними називаються балки, що лежать більше ніж на двох опорах і які при цьому не мають проміжних шарнірів.

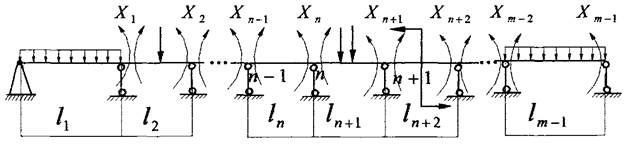
При цьому одна із опор є шарнірно-нерухома, для сприйняття осьових навантажень, а всі інші рухомі.

Опори прийнято нумерувати зліва направо, позначаючи крайню ліву опору №"О".