Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 5

Таким чином при аналітичному розв’язку задачі знаходження величин  і  необхідно послідовно двічі проінтегрувати рівняння (1).

Проінтегрувавши один раз рівняння (1) будемо мати вираз для визначення кута повороту поперечного перерізу:

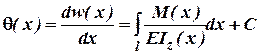, що включає в себе одну довільну константу.

Проінтегрувавши другий раз рівняння (1) отримаємо вираз для визначення прогину:

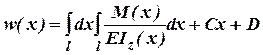, який включає в себе вже дві довільні постійні  і.

Величина  згину визначається із епюри для недеформованої балки. Константи  і  визначаються із граничних умов, тобто із умов закріплення балки:

1. Якщо балка жорстко закріплена, то в місці закріплення кут повороту і прогин будуть дорівнювати нулю:

;

2. Якщо балка знаходиться на двох опорах (шарнірах), то прогин на опорах буде дорівнювати нулю.

Розглянемо два приклади по визначенню переміщень методом інтегрування ДР зігнутої вісі балки:

Приклад 1.

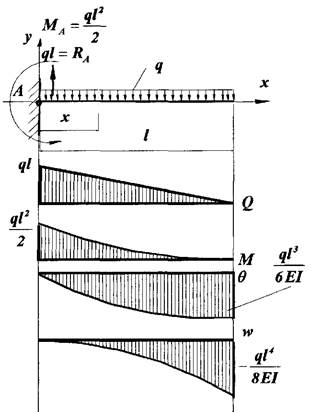Дано:;;

Визначити:, – ?

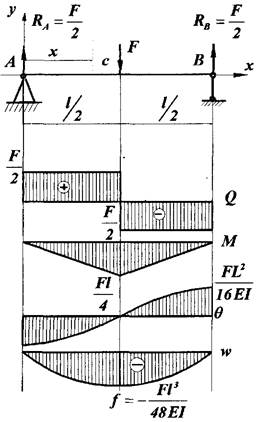
Розв 'язок:

Запишемо рівняння моментів у довільній точці по довжині балки:

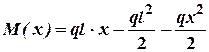
Запишемо ДР зогнутої вісі балки:

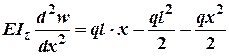
1. Проінтегруємо цей вираз один раз:

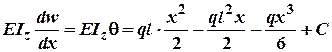
2. Проінтегруємо цей вираз другий раз:

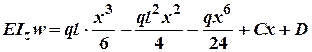
При  із граничних умов можемо записати, що  і, а відповідно  і  дорівнюють нулю. Відтак:

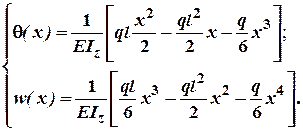
При:

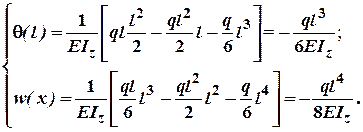
Таким чином, крива кутів повороту являє собою параболу третього порядку (або кубічну параболу), знак "–" вказує на те, що поперечний переріз повертається за ходом годинникової стрілки, а її кривизна направлена випуклістю вгору. Крива пружної лінії вісі балки являє собою параболу четвертого порядку, а знак "–" вказує на те, що прогин відбувається в напрямку протилежному напрямку осі  і, оскільки стиснуті волокна балки будуть внизу, то її випуклість буде направлена вгору.

Записавши умову жорсткості 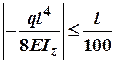 знаходимо, а знаючи, що 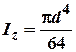 визначимо діаметр балки. Такий розрахунок наз. розрахунком розмірів балки, виходячи з умови жорсткості.

Приклад 2:

Дано:;;

Визначити: – ?;– ?

Рішення.

1. Записуємо вираз для згинаючого моменту в довільній т.

.

2. ДР для цього випадку буде:

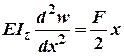
3. Інтегруємо ДР два рази:

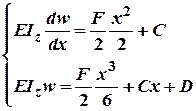
Із граничних умов (умов закріплення) маємо:

При. Із другого рівняння знаходимо.

При. Із першого рівняння.

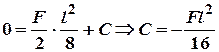Таким чином, рівняння для визначення кутів повороту і прогину поперечного перерізу для двохопорної балки запишуться так:

1) При:; 2) При:;

Диференційні залежності між, , ,

Із рівняння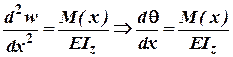. Продиференціювавши його по  і врахувавши, що  будемо мати: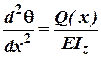. Таким чином маємо дві групи рівнянь (ДР):

        

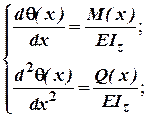
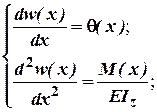
аналогічних залежностям, на основі яких були отримані правила для побудови епюр і.

Самостійно:Вивчити правила побудови епюр для, , ,.с. 275-276.

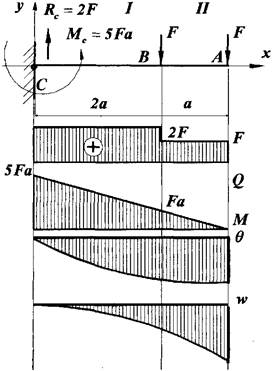
Диференційне рівняння зігнутої осі балки

Приклад 1

Визначити максимальний прогин і кут повороту поперечного перерізу в точках  і, якщо сила, що діє на брус,. Переріз має форму двотавра, матеріал – сталь.

Розв 'язок.

1. Запишемо рівняння для згинаючого моменту на 1-й ділянці.

2. Диф. рівняння зігнутої осі бруса.

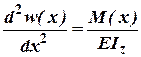
3. Інтегруємо вираз для згинаючого моменту два рази:

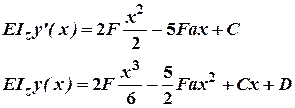
4. Для першої ділянки ():

При:

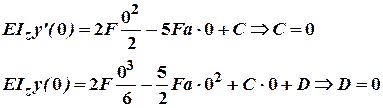
При:

;

.

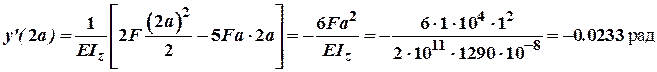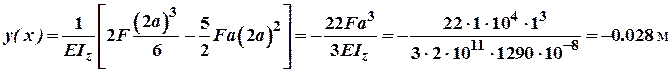5. Для другої ділянки ():

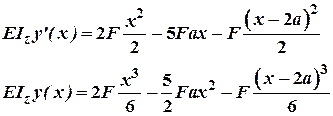
При:

;

.

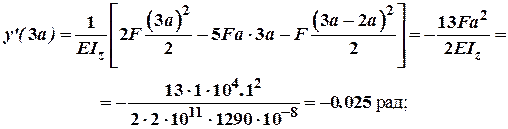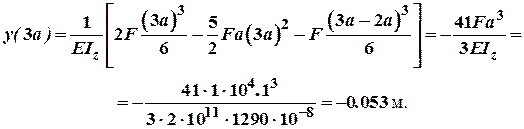Домашнє завдання:

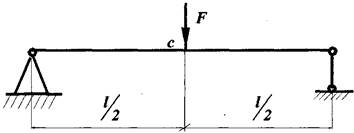Стальна балка довжиною прямокутного поперечного перерізу навантажена посередині прольоту  зосередженою силою.

Визначити найбільший кут повороту перерізу і найбільший прогин.

Лекція № 5

Визначення переміщень по методу початкових параметрів.

План лекції:

1. Загальні положення розв'язку задач.

2. Геометричні та статичні початкові параметри.

Література : [1] - ст. 276 - 290, [2] - ст. 365 - 370.

Метод початкових параметрів, також як і метод інтегрування ДР вигнутої осі балки служить для визначення прогинів і кутів повороту тільки в балках, але цей метод має суттєву перевагу, оскільки число const, що визначаються по цьому методу, може дорівнювати максимум двом при любій схемі завантаження балки і любій кількості ділянок.