Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 10

Для довідки: в трикутниках, що обмежені параболічною залежністю

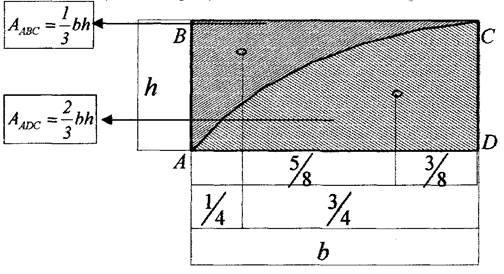
Порядок розрахунку задачі за методом Верешагіна.

1. Будуємо епюру згинаючих моментів від дії зовнішніх сил для заданої пружної системи.

2. Вводимо одиничну систему також, як і по методу Мора будуємо епюру одиничних моментів.

3. Обидві системи одночасно розбиваємо на ділянки. Для кожної ділянки розраховуємо площу силової епюри і ординату під її центром ваги на епюрі одиничних моментів.

4. Якщо силова епюра і ордината на одиничній епюрі розміщується по одну сторону від бази, то добуток береться із знаком "+", в противному випадку "-". Знак "-" в кінцевому випадку говорить про те, що шукане нами переміщення відбувається в напрямку, що є протилежним до попереднього (напрямок дії одиничного навантаження нами заданий).

Приклад 1.

Дано:

Визначити:–?

Розв'язок.

;;

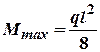де;

(см⁴), де

Приклад 2

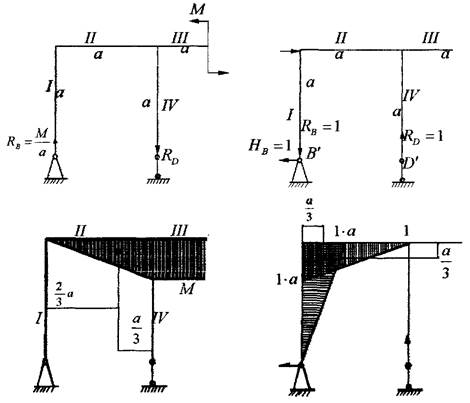
Дано:

Визначити:–?

Розв'язок.

1. Будуємо епюри силової і одиничної систем.

2. Так як тільки на ділянці II співпадають епюри на силові і на одиничних системах, то переміщення яке визначається, буде залежати тільки від їх перемноження, тобто:

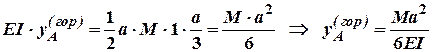
Так як значення  має знак "+", то переміщення т.А відбувається в напрямку дії сили, тобто вправо.

Якщо візьмемо площу на одиничній епюрі, а ординату на силовій епюрі, то:

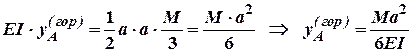
Але тільки в випадку, коли силова і одинична епюри обмежені прямими лініями - немає значення де брати площу, а де ординату.

Множення епюр по методу Верещагіна необхідно проводити з урахуванням знаків.

Приклад 3.

Дано: – діаметр стержня на всіх трьох ділянках; G; Е; F; М; а.

Визначити: – ?

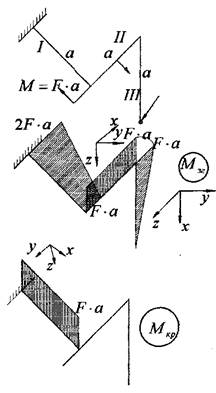
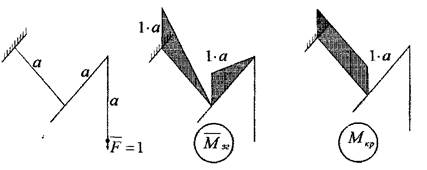
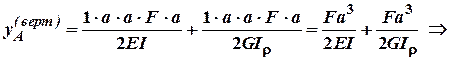
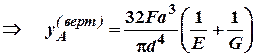, де;.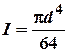

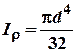Потенційна енергія деформації.

П.Е.Д. є квадратичною функцією переміщень і через це завжди виступає як величина додатня. П.Е.Д. чисельно дорівнює роботі зовнішніх сил.

і тому, по аналогії з роботою зовнішніх сил буде визначатись як:

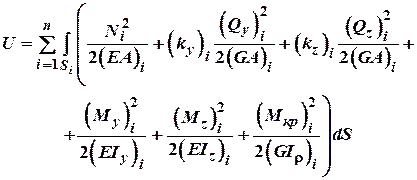
Відтак для плоскої системи:

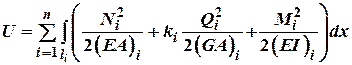
Якщо система складається із криволінійних стержнів, то в інтегральних виразах замість  ставиться.

Для балок потенційна енергія дорівнює:

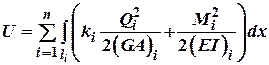
При дії на стержневу систему кінцевої довжини тільки осьових сил П.Е.Д. буде дорівнювати:

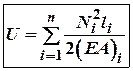
Приклад 1.

Визначити:, що накопичена в пружній системі, якщо відомо

Розв'язок.

1. Значення діючого моменту на ділянці беремо із епюри.

2. Так як момент, що діє в межах одної ділянки постійний і її жорсткість постійна, то:

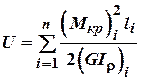
Приклад 2.

Дано:

см; кг/см²; кг/см²

Визначити:– ?

– П.Е.Д., що утворена дією;

– П.Е.Д., що утворена дією.

Розв'язок.

;

;

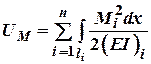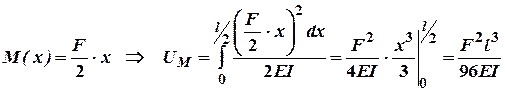
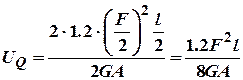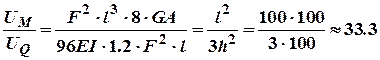
В балках і практично в усіх пружних плоских системах П.Е.Д. розраховується тільки від згинаючого моменту, оскільки  набагато менша.

Таким чином:

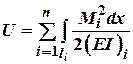
В просторовій системі п.е.д. дорівнює:

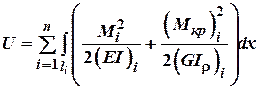
Приклад 3

Визначити переміщення за допомогою п.е.д.

Так як П.Е.Д. чисельно дорівнює дійсній роботі зовнішніх сил, то із попереднього прикладу із виразу для визначимо переміщення, наприклад, для т.А.

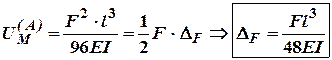
Лекція №9

Побудова епюр внутрішніх силових факторів для плоских кривих брусів.

План лекції:

1. Аналітичні залежності по відзначенню внутрішніх силових факторів.

2. Диференційні залежності між,  і.

3. Приклади визначення внутрішніх зусиль та переміщень в криволінійних брусах.

Література : [1] - ст. 66 - 75, [2] - ст. 580 - 609.

Ми будемо розглядати плоскі криві бруси у яких силова, геометрична і вісь симетрії лежать в одній площині.

При такому навантаженні бруса в його поперечних перерізах виникають три внутрішніх силових фактори:

1. Поздовжня сила 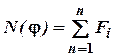 всіх зовнішніх сил на дотичну до бруса в точці, що розглядається;

2. Поперечна сила 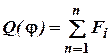 всіх зовнішніх сил  на нормаль до осі (поздовжньої) стержня;

3. Згинаючий момент 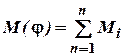 всіх зовнішніх силових факторів по одну сторону від відсіченої частини стержня.

Правило знаків для поздовжніх та поперечних сил таке ж саме, як і для прямого брусу. Згинаючий момент вважається додатнім, якщо він збільшує кривизну бруса. При побудові епюр величини сил  і, згинаючих моментів  відкладаються по нормалі до геометричної осі бруса.