Прості види деформування. Складний згин, умови міцності. Косий згин, умови міцності, страница 18

Самостійно:(Писаренко ст. 507 - 508.) Про вибір матеріалу і раціональних форм поперечних перерізів для стиснутих стержнів.

Лекція 13

Пружні коливання

План лекції:

1. Класифікація коливань. Явище резонансу.

2. Гармонічні коливання з одним ступенем вільності.

3. Розрахунки періоду і частоти коливань, виходячи із умов міцності і жорсткості системи.

4. Вимушені коливання пружних систем з одним ступенем вільності.

Література : [1] - ст. 515 - 546. [2] - ст. 686 - 700.

Вібрації споруд, машин, елементів конструкцій, електромагнітні коливання, звукові і ультразвукові – всі ці несхожі одні на інші явища об'єднуються методами математичної фізики в одне загальне вчення про коливання.

Розрізняють два основних класи коливальних процесів: періодичні і неперіодичні, а також майже періодичні.

Періодичниминазиваються коливання, які описуються функцією  з періодом, для якої виконується залежність.

Неперіодичними функціямиколивань називаються всі інші функції, що не задовольняють вказаній умові.

Майже періодичними функиіямиє функції, що визначаються умовою  , для любого, при тому, що  і  визначені, постійні величини.

До класу періодичних коливань відносяться коливання, закон зміни фізичних величин у яких відбувається за -ом чи -ом.

До класу неперіодичних коливань відносяться всі інші види коливань, що не підкоряються попереднім умовам. Це можуть бути затухаючі чи наростаючі випадки -их чи -их коливань, що математично записуються таким чином:

, де, , ,  є величинами постійними, а  – час.

Класифікуючи механічні коливання, їх розділяють на чотири типи: власні, вимушені, параметричні і автоколивання.

– Амплітуда власних коливань та їх швидкість визначається з граничних умов. При цьому їх період () і частота залежать тільки від фізичного складу самої системи і називаються власною частотою (періодом) коливань системи. Основною особливістю власних коливань є те, що вони завжди будуть затухаючими.

– Період, частота і амплітуда вимушених коливань залежать тільки від збуджуючого ці коливання зовнішнього фактора.

– Коли частота власних коливань системи дуже близька, чи співпадає з частотою збуджуючої зовнішньої сили, то амплітуда вимушених коливань такої системи значно зростає - це явище носить назву резонансу.

При дослідженні коливальних рухів в пружних системах важливо знати, яке число незалежних параметрів визначає стан системи в кожен момент часу. Число таких параметрів визначається числом степенів вільності.

В найпростіших випадках, коли стан системи може бути визначений за допомогою одної величини, то такі системи називаються системами з одним ступенем вільності.

В цьому курсі ми будемо розглядати з вами вільні та вимушені гармонічні коливання пружних систем з одним ступенем вільності.

1. Вільні гармонічні коливання з одним ступенем вільності

Як приклад розглянемо коливання тіла вагою, що підвішене на пружині (її вагою нехтуємо).

ДР коливання такої системи отримаємо використовуючи відомий принцип д'Аламбера, прирівняємо до нуля суму проекцій всіх діючих сил на тіло на вісь.

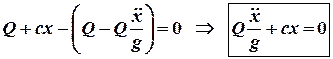          (1)

У ДР (1) перший доданок – це сила inepuiL а другий – сила пружності. Запишемо його так:

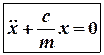.                                             (2)

Це ДР гармонійних коливань.

Позначимо: і запишемо:,                                                (3)

де  – друга похідна від шляху, що пройшло тіло вагою за час  (або іншими словами це - прискорення)

З іншого боку 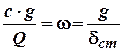               , де      – жорсткість пружини, що чисельно дорівнює силі, яка визвала розтяг пружини рівний одиниці її довжини;

– прискорені сили тяжіння;

– статична деформація розтягу пружини під дією підвішеного тіла вагою.

Таким чином, власна частота (вона ще називається круговою частотою) гармонічних коливань буде дорівнювати:

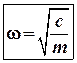чи так 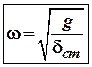                                (4)

Очевидним розв'язком рівняння (3), що встановлює зв'язок між ординатою тіла і часом буде: