Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 32

В i-й строке стоят места (ранги), данные i-м экспертом ранжируемым объектам. Все n объектов упорядочиваются в соответствии величиной , определяемой по формуле . На первое место ставится объект, у которого   минимально. Степень согласованности определяется коэффициентом конкордации , где n – число объектов, N – число экспертов.

12.5.2. Нестрогое ранжирование.

Задача состоит в сопоставлении системе нестрогой ранжировки, т.е. объекты могут быть равноценными с одинаковыми рангами. Коэффициент конкордации 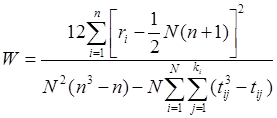 , где k_i – число групп равных рангов, введенных i-м экспертом.

Статистическую значимость ранжировки проверяют следующим образом. Выбирают вероятность ошибки P_ош. Предполагают, что величина N(n-1)W имеет - распределение с (n-1) степенью свободы. По таблицам находят значение . Если коэффициент W, полученный при реализации экспертизы, не меньше , то полученную ранжировку считают статистически значимой.

Выше предполагалось для простоты, что эксперты имеют одинаковую компетентность.

Вопросы итогового собеседования.

1.  Постановка задачи выбора в условиях стратегической неопределенности.

2.  Основные понятия теории игр. Парная антагонистическая игра в задаче выбора в условиях стратегической неопределенности.

3.  Игры с седловой точкой в задаче выбора в условиях стратегической неопределенности.

4.  Решение игры в смешанных стратегиях в задаче выбора в условиях стратегической неопределенности.

5.  Сведение игры в смешанных стратегиях к задаче линейного программирования в задаче выбора в условиях стратегической неопределенности.

6.  Имитационный метод Брауна-Джонсона в задаче выбора в условиях стратегической неопределенности.

7.  Постановка задачи выбора в условиях природной неопределенности.

8.  Статистические игры без экспериментов с известными априорными вероятностями состояний природы.

9.  Статистические игры без экспериментов с неизвестными априорными вероятностями состояний природы и возможностью выдвижение гипотез.

10.  Статистические игры без экспериментов при отсутствии информации о состоянии природы.

11.  Статистические игры с единичным идеальным экспериментом.

12.  Статистические игры с единичным неидеальным экспериментом.

13.  Решающие функции в статистических играх.

14.  Постановка задачи выбора в условиях риска.

15.  Структура выбора в задачах принятия решения в условиях риска.

16.  Модель баесова риска в задачах принятия решения.

17.  Модель правдоподобия в задачах принятия решения.

18.  Задача достижения нечетко определенной цели.

19.  Задача нечеткого управления при нечетких ограничениях.

20.  Некритериальные задачи нечеткого выбора.

21.  Стабилизация экспертной сети в задачах экспертного выбора.

22.  Численные оценки экспертизы в задачах экспертного выбора.

23.  Метод «Делфи» в задачах экспертного выбора.

24.  Строгое ранжирование в задачах экспертного выбора.

25.  Нестрогое ранжирование в задачах экспертного выбора.

Литература

1.  Перегудов Ф.И, Тарасенко Ф.П. Введение в системный анализ. – 1989. (LIBRARY\BOOKS\Peregudov\...)

2.  Зяблицкий А.В. Бюрократизм в эргатических системах. – 1998. /реферат по дисциплине «Алгоритмы и методы принятия решений». (LIBRARY\ MET_DOC\WYB.98\REFERATS\burokrat.arj)

3.  Мерсер Д. ИБМ: управление в самой преуспевающей корпорации мира. – 1991.

(Library.99\BOOKS\manager\ibm.exe)