Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 13

*  Отношение E - диагональное:  - "i,j: <x_i,x_j> ÎE,  для i=j;

- a_ij(E)={1: i=j; 0: i ¹ j;

- граф с петлями у каждой вершины, без дуг.

- E⁺(x)= E^-(x)={<x,x>: xÎE}.

6.3.Свойства отношений.

·  рефлексивность: E Í R, E - диагональное;

"x ÎA: xRx; xÎR⁺(x) & xÎ R^-(x) "x ÎA;

·  антирефлексивность:R Ç E = Æ;  xRy Þ x¹y; xÏR⁺(x) & xÏR^-(x) "x ÎA;

·  симметричность:R Í R^-1;  xRy Þ yRx; "i,j: a_ij= a_ji;

"x ÎA: R⁺(x)= R^-(x).

·  асимметричность:R Ç R^-1= Æ; xRy или yRx;

"x ÎA: xÎR⁺(x) Þ xÏR^-(x).

·  антисимметричность:R Ç R^-1 Í E; xRy & yRxÞ x=y;

a_ij &a_ji=0, i¹j; "x ,yÎA: y Î R^-(x) & x¹y Þ xÏR^-(x).

·  транзитивность:R² Í R; xRy & yRzÞ xRz;

индукция для n альтернатив.

·  ацикличность:R^k Ç R^-1= Æ;

xRz₁ & z₁Rz₂ & ... & z_k-1Ry Þ x¹y.

·  отрицательно транзитивное:дополнение R транзитивно.

·  сильно транзитивное:отрицательно транзитивное и транзитивное.

6.4. Отношения эквивалентности, порядка, доминирования.

6.4.1. Отношение эквивалентности.

<~,(XxX)>; рефлексивность, симметричность, транзитивнсть.

*  "x,y ÎA: xÎR⁺(x); x~y Þ R⁺(x) ~ R⁺(y);

R⁺(x) Ç R⁺(y) = Æ Þ R⁺(x) = R⁺(y).

*  A= È_i A _i  & A _i Ç A _j = Æ, i¹j; Card({A _i}=n<¥.

6.4.2. Отношения порядка.

·  "x,y ÎA:  нестрогий “£”:

рефлексивность & антисимметричность & транзитивность.

·  строгий “<”:

антирефлексивность & асимметричность & транзитивность.

·  линейный: "x,y ÎA: x<y или x=y или x>y.

6.4.2. Отношения доминирования.

*  “>>” : антирефлексивность & асимметричность.

*  граф предпочтений.

6.5. R-оптимальность (формализация отношения «лучший»).

<R,(XxX)>,       xÎX & "yÎX: xRy Þ x - максимум по R;

xÎX & "yÎX: yRx Þ x - минимум по R;

xÎX & "yÎX: x`R  y Þ x - миноранта по R;

xÎX & "yÎX: y`R  x Þ x - мажоранта по R;

X⁺(R) - множество максимумов;   

X₊(R) - множество мажорант;

X^-(R) - множество минимумов;

X_-(R) - множество минорант.

Теорема: X⁺(R) = X^-1(R^-1);    X^-(R) = X^-(R^-1);

X₊(R) = X_-(R^-1);     X_-(R) = X₊(R^-1);

X⁺(R)= X₊(R^d);      X^-(R) = X_-(R^d).

R-оптимальные альтернативы:

X^R = X₊(R) - множество недоминируемых по R элементов (R-оптимальных элементов).

X_R = X⁺(R) – множество абсолютно лучших альтернатив.

6.6. Функции выбора.

А,  2£½A½£¥, АÊX, ХÊY, Y - выбор из Х.          Y=C(X), C(X)ÎÃ,

6.6.1. Блокировка и предпочтение.

АÊX, (XxX)ÊR - бинарное отношение, сопоставим функцию выбора.

C^R(X)={xÎX: "yÎX: y`R  x} - блокировка;

C_R(X)={xÎX: "yÎX: xRy} - предпочтение.

Теорема: C_R = C_R^d & C_R = C^Rd.   R^d - двойственное.

Из двух отношений можно рассматривать только одно.

C^R -^df функция выбора порожденная R.

Теорема: Произвольная функция выбора С не обязательно совпадает с некоторой C^R.

X={x,y}; C(x)=^dfx, C(y)=^df Æ, C(x,y)=^df{x,y}.

Пусть $R: C=C^R Þ x`R  x, т.е. неверно, что xRx.

C ^R(y)= Æ Þ yRy Þ неверно, что y`R  y Þ yÏ C^R(X), что противоречит определению С.

Теорема:"X: C ^R(y) ¹ Æ Û R - ациклично.

6.6.2. Логические формы функций выбора (ЛФВ).

X, Y=C(X), , X={x₁, …, x_N}.

Установим биекцию между 2^N подмножествами X и 2^N векторами длины N с компонентами 0, 1:

 

      Æ

Определим   по правилу

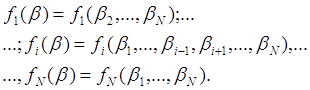
ЛФВ(С) =^df <f₁, …, f_N> - логическая форма функции выбора.

Теорема. Задание ЛФВ(С) эквивалентно заданию С.

6.6.3. Классы функций выбора.

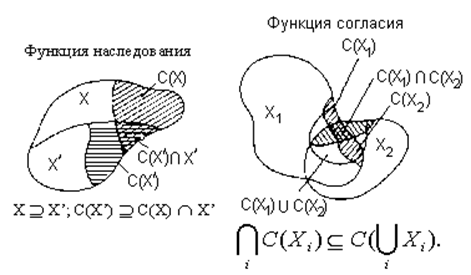
Функция, независимая от отвергнутых альтернатив:

X Ê X’ Ê C(X) Þ C(X) = C(X’).

Функция Плотта: С(X₁ È X₂) =С(С(X₁)ÈС(X₂)).

Функция отбрасывания:

Функция предпочтения:

Cумматорная функция: С(X₁ È X₂) =С(X₁)ÈС(X₂).

Мультипликаторная функция: С(X₁ Ç X₂) =С(X₁) ÇС(X₂).

Монотонная функция: X₁ Í X₂ Þ С(X₁) Í С(X₂).

6.7. Групповой выбор. («Ум - хорошо, а два – лучше»)

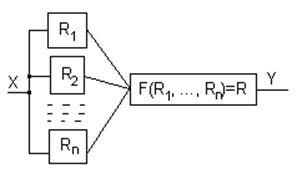
·  X,  R - ?.