Другие предметы \ Методы и алгоритмы принятия решений

Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 29

1-я	6300	6870	6120	6980	6780	6780	6780
2-я	6900	7130	6690	6750	6560	6700	6930
	6720	6630	6660	7150	6950	7230	7240
	6720	6950	6960	7280	7120	6690	7070
	7090	6800	7000	7070	6700	7140
	6950	6590	6890	6910	6630	7220

Можно ли утверждать, что обе партии проволоки требуемого качества, и результаты испытаний следует объяснить случайностью выборки?

11. Задачи выбора в условиях

нечеткой неопределенности.

Конспект

· Неопределенность – неоднозначность последствий.

11.1. Нечеткие множества и нечеткие отношения.

, нечеткое множество:

- функция принадлежности.

Æ; X.

; ;

- четкое множество уровня нечеткого множества А в Х.

; ;

, где .

Отношение: . - матричное задание.

; ;

; .

- композиция. ; .

R – рефлексивно .

R – антирефлексивно .

R – симметрично, .

R – антисимметрично , , .

R – транзитивно

Транзитивное замыкание: .

Нечеткое отношение: ,

; , .

, ;

, .

R – рефлексивно , .

R – антирефлексивно ,;

R – рефлексивноR’ – антирефлексивно.

R – симметрично .

R – антисимметрично

R – транзитивно .

Транзитивное замыкание: .

Транзитивное замыкание транзитивно, транзитивное отношение совпадает со своим транзитивным замыканием.

11.2. Задача достижения нечетко определенной цели.

Х – множество альтернатив, G – нечеткое подмножество Х, нечеткая цель; .

, - нечеткие ограничения.

- одинаковой важности. .

- решение.

n – целей, m –ограничений, ,

11.3. Задача нечеткого управления при нечетких ограничениях.

Х – множество состояний системы;

U – множество управлений системой;

, , - детерминированная система управления.

- нечеткие ограничения управления.

- нечеткая цель управления.

Т.е. нужно выбрать последовательность управлений , которая «удовлетворяет» нечетким ограничениям и «обеспечивает» достижение нечеткой цели.

Т.к. , то . В соответствии с подходом Беллмана-Заде нечеткое решение задачи может быть представлено в виде нечеткого подмножества с функцией принадлежности .

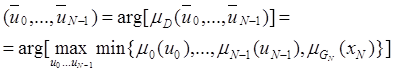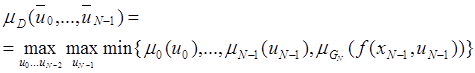Имеет место следующее равенство для величины , не зависящей от , и произвольной функции : .

Преобразуем

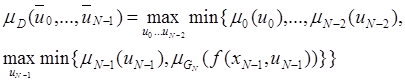и введем обозначение

- функция принадлежности нечеткой цели для задачи управления на интервале , соответствующая заданной цели управления на интервале , т.е. есть максимальная степень достижения цели в случае, когда на (N-2)-м шаге система оказалась в состоянии .

Поскольку , то величина есть максимальная степень достижения цели в случае, когда система оказалась (после (N-2)-х шагов управления) в состоянии x_N_-2 и на (N-1)-м шаге было выбрано управление u_N_-2. Выбор u_N_-2 на (N-1)-м шаге должен обеспечить максимальное значение величины