Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 15

7.2. Методы шкалирования предназначены для обработки данных о попарных сходствах, связях или отношениях между анализируемыми объектами с целью представления этих объектов в виде точек некоторого координатного (критериального) пространства.

 - мера сходства или различия объектов i и j; величина, полученная эмпирически.

 - расстояние; аксиомы - , , , .

 - значение признака k у объектов i и j соответственно (координаты i и j).

.

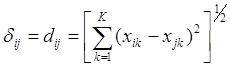 - симметричная квадратная матрица с мерами различия пар объектов (i,j), из которой необходимо получить координаты x_ik и x_jk. i = 1,…,I; j=1,…,J; I=J; k=1,…,K.

 Метод Торгерсона.

Без потери общности .

Строим :

;

, , .

Теорема Торгерсона. Если 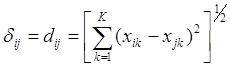, то .

Получаем матричное уравнение . Пусть Т_(kxk)– ортогональная матрица, ,  - тоже решение: . За счет подбора Т осуществляется поиск интерпретируемого варианта решения, если известно К.

К – не известно, находятся собственные значения  и располагаются в порядке убывания. Если последовательность «стабилизируется» на К+1 значении, следовательно, число осей равно К.

Индивидуальные задания

Привести пример процедуры обоснования решения для детерминированной задачи выбора:

1.  Отыскание условного экстремума с ограничениями типа равенств.

2.  Задача линейного программирования.

3.  Задача квадратичного программирования.

4.  Задача выпуклого программирования.

5.  Задача с сепарабельными критериальными функциями и линейными ограничениями.

6.  Задача геометрического программирования.

7.  Задача дискретного программирования.

8.  Задача целочисленного линейного программирования

9.  Задача дискретного программирования методом Беллмана.

10.  Метод ломаных Эйлера решения простейшей вариационной задачи.

11.  Метод Галеркина решения простейшей вариационной задачи.

12.  Метод вариаций решения простейшей вариационной задачи.

13.  Простейшая задача оптимального управления.

14.  Свертка в многокритериальной задаче.

15.  Условная максимизация в многокритериальной задаче.

16.  Метод уступок в многокритериальной задаче.

17.  Метод идеальной точки в многокритериальной задаче.

18.  Формирование множества Парето в многокритериальной задаче.

19.  Теоретико-множественный R-оптимальный выбор.

20.  Теоретико-множественный выбор на основе логической формы функции выбора.

21.  Теоретико-множественный выбор на основе функции наследования.

22.  Теоретико-множественный выбор на основе функции согласия.

23.  Теоретико-множественный выбор на основе функции Плотта.

24.  Теоретико-множественный выбор на основе функции, независимой от отвергнутых альтернатив.

25.  Теоретико-множественный выбор на основе функции отбрасывания.

26.  Теоретико-множественный выбор на основе функции предпочтения.

27.  Теоретико-множественный выбор на основе группового выбора.

28.  Выбор на основе функции полезности в критериальном пространстве, построенном по следующей матрице различий.