Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 31

1.   - оценка i-й альтернативы j-м экспертом (i=1,…,m; j=1,…,n).  - некоторая статистика в предположении, что  - случайные величины, в частности,  - выборочное среднее. Степенью согласованности мнений экспертов может служить дисперсия . Статистическая значимость результатов определяется вероятностью ошибки Р_ош. Интервал, в который попадает оцениваемая альтернатива  с вероятностью 1-Р_ош: . При условии, что  распределена нормально с центром  и дисперсией , , где величина t имеет распределение Стьюдента с (n-1)-й степенью свободы.

2.  Если альтернатива оценивается набором признаков , где k – номер признака, экспертом дополнительно оценивается степень важности  каждого показателя. Тогда .

3.  Группа экспертов может быть неоднородна.  - степень компетентности j-го эксперта может быть оценена этой же экспертной группой - 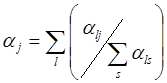, где  - оценка l-м экспертом   j-го эксперта, . Итоговая оценка: .

4.  , ,  - оптимистическая, наиболее вероятная и пессимистическая оценки j-м экспертом k-го признака i-й альтернативы. , здесь  - определяются эмпирически (, , ,  - по одной методике, , , ,  - по другой методике).

12.4. Метод «Делфи».

Основная идея этого метода состоит в том, что критика благотворно влияет на эксперта, если она психологически не связана с персональной конфронтацией. Поэтому если проводить оценку альтернатив в несколько туров, сообщая после каждого его полные итоги и сохраняя анонимность участников, то эксперты склонны не только критиковать, но и прислушиваться к критике, относящейся к ним лично. Устранение психологических трудностей, связанных с персональной критикой, придает самой критике большую деловитость, объективность, она легче воспринимается Все это приводи г к тому, что обычно оказывается достаточно следующих четырех этапов:

1) раздача анкет, сбор оценок, их обобщенное представление с указанием разброса мнений;

2) сообщение итогов и запрос объяснений причин индивидуального отклонения от средней или медианой оценки первой итерации;

3) сообщение всех объяснений и запрос контраргументов на них;

4) сообщение возражений и запрос новых оценок альтернатив, если эксперт пожелает их изменить, нахождение окончательного итога.

Вся работа проводится под руководством отдельной управляющей группы, в которую входят системный аналитик и лицо, принимающее решения; анонимность экспертов сохраняется до конца работы (а по желанию экспертов - и после ее окончания).

Весь интервал допустимых значений оцениваемой величины разбивается на k интервалов ; эксперт оценивает вероятность попадания оцениваемой величины в каждый из интервалов; по результатам составляется таблица, где p_ij – оценка вероятности попадания

Оцениваемой величины в j-й интервал, данная i-м экспертом. На основании этой таблицы определяется мнение экспертов о попадании оцениваемой величины в каждый из интервалов t_j:  (. . 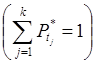Результирующей оценкой является медиана построенного распределения q₂, определяемая из условия . Помимо q₂ вычисляется диапазон квантилей , где  ; . Эмпирически установлено, что процедуру  можно прекращать, когда диапазон квантилей уменьшился в 1,6 раза по сравнению с первоначальным.

12.5. Ранжирование.

12.5.1. Строгое ранжирование.

Задача состоит в сопоставлении оцениваемой системе одной перестановки. Результаты опроса экспертов сводятся в таблице