Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 12

4.  Минимизировать 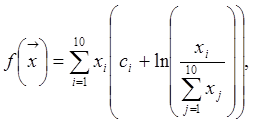 где с₁ = -6,089; с₂ = -17,164; с₃ = - 34,054; с₄=-5,914; с₅=-24,751; с₆=-14,986; с₇=-24100; с₈=-10,708; с₉=-26,662; с₁₀=-22,179.

Ограничения:    

5.  Максимизировать

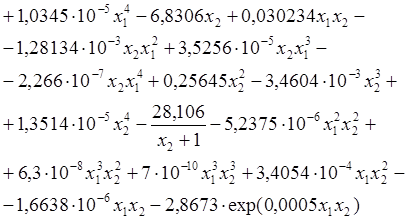
при ограничениях  ,

, ,

.

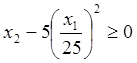6.  Минимизировать 

Ограничения:   

7.  Минимизировать

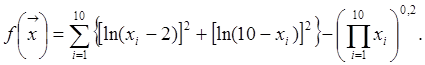
Ограничения: 2,001<x_i<9.999; i=1,…,10.

8.  Минимизировать

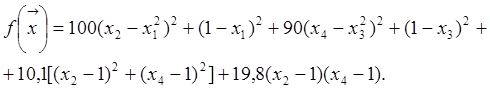
Ограничения:

9.  Минимизировать  

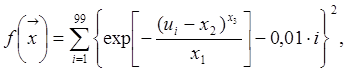
Ограничения: ;  .

10.  Минимизировать  

Ограничения: ; .

11.  Минимизировать

12.  Минимизировать

13.  Минимизировать

14.  Минимизировать

15.  Минимизировать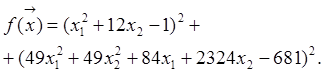

16.  Минимизировать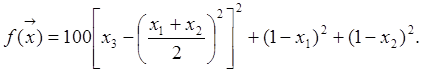

17.  Минимизировать

18.  Минимизировать ,

5. Многокритериальный выбор

Конспект

·  Определенность – однозначность исхода последствий.

5.1. Задача многокритериального выбора

А,  2£½A½£¥, АÊX, ХÊY, Y - выбор из Х.

YÍХ Y=C(X), C(X)ÎÃ,

М=< s,p > - механизм выбора.

s - структура над А (сведения об альтернативах).

p - правило выбора (инструкция как из Х, используя s, выделить Y).

R - линейно упорядочено:  "x,yÎX: x < y Ú x = y Ú x > y,

“<” -отношение предпочтения.           

q₁,q₂ , ... ,q_p - критерии; s: q_i: A ® R;      "xÎА "i=1...p $ rÎR: r= q_i(x);

" x₁,x₂ÎА "i=1...p: x₁ предпочтительнее x₂ Û^df q_i(x₁) > q_i(x₂).

p: q=q(q₁(x), q₂(x), ..., q_p(x)) - суперкритерий; <s, p> - df  С().

 

5.2. Методы решения суперкритериальных задач.

5.2.1. Свертка (сведение к однокритериальной задаче).

 - суперкритерий.

 - аддитивная свертка;

 - мультипликативная свертка.

 - «подтягивание отстающего»

(максминная свертка).

·  Неоднозначность упорядочения точек в многомерном пространстве, суперкритерий - упорядочивающая функция (проблема  многомерности);

·  слабая определенность по весовым коэффициентам;

·  срыв монотонности.

5.2.2. Условная максимизация.

Неравнозначность критериев, есть главный критерий.

.

5.2.3. Метод уступок.

s: q₁ ³ q₂ ³ ... ³ q_p; ³ - линейный порядок по степени вложенности.

Dq₁ - “уступка”, условие увеличения q₂,

Dq₁ ,   q₂ Þ х₂^*,              могут быть и другие сценарии

Dq₂ ,   q₃ Þ х₃^*, и т.д.                         p

...................................

<s, p>

5.2.4. Метод идеальной точки.

·  известны области  значений частных критериев q_i (часто - верхние и нижние границы),

Q_i - уровни притязаний;

 - цель, опорная точка, идеальная точка (область).

·  найти альтернативу в Х, которая наиболее близка цели (по имеющимся критериям).

s: метрика на Х –

.

,

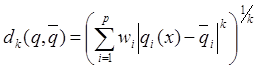a_i  - нормирующие, весовые;   a_{p +1}  - важность слагаемых.

Возможна модификация, если на q_i есть ограничения «больше, меньше, равно».

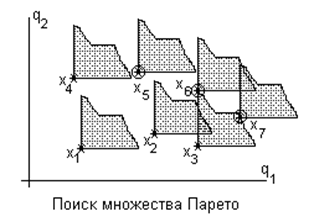5.2.5. Множество Парето.

·  Отказ от поиска наилучшей альтернативы.

·  Одна альтернатива предпочтительнее другой,  если первая по всем критериям лучше второй.

·  Несравнимые альтернативы.

·  Формирование множества Парето.

·  Проблема выбора единственной альтернативы.

6. Теоретико-множественный выбор

Конспект

·  Определенность – однозначность исхода последствий.

6.1. Задача бинарного выбора

А,  2£½A½£¥, АÊX, ХÊY, Y - выбор из Х, АÊX, (XxX)ÊR - бинарное отношение.

s: 1. "xÎА: критерий  х отсутствует;

2. "(x,y)ÎА: (x  предпочтительнее y) Ú (x равноценно y) Ú (x несравнимо с y);

3.  предпочтительность (x,y) не зависит от других пар.

6.2. Способы задания бинарного отношения.

(XxX)ÊR, <R,(XxX)>;

- перечисление всех пар <x,y>ÎR;

- матричный: ½Х½< ¥, (XxX)ÊR, X={x_i: i=1,...,n}, [a_ij], a_ij=1 Û <x,y> ÎR, a_ij=0 Û <x,y> ÏR;

n! эквивалентных s.

- графом;

- сечениями:  R⁺(x)={yÎX: <y,x> ÎR} - верхнее сечение;

R^-(x)={yÎX: <x,y> ÎR} - нижнее сечение.

*  Отношение U - полное:  - "x_i,x_jÎX: <x_i,x_j> ÎU;

- "i,j: a_ij(U)=1;

- граф полный с петлями в каждой вершине.