Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 19

9. Выбор в условиях природной неопределенности.

Конспект

·  Неопределенность – неоднозначность последствий.

Злонамеренность противника в стратегических играх; стохастическая неопределенность, природа; теория статистических решений, игры статистика с природой.

9.1. Постановка задачи.

А,  2£½A½£¥, АÊX, ХÊY, Y - выбор из Х.

YÍХ Y=C(X), C(X)ÎÃ, М=< s,p > - механизм выбора.

s - структура над А (сведения об альтернативах).

,  - стратегии 1-го игрока («мы», активная сторона).

,  - состояния (стратегии) природы (пассивная сторона).

 - матрица выигрышей.

,  - вектор вероятностей состояний природы.

X\П	П1	П2	…	Пj	…	Пn
x1	a11	a12	…	a1j	…	a1n
…	…	…	…	…	…	…
xi	ai1	ai2	…	aij	…	ain
…	…	…	…	…	…	…
Xm	am1	am2	…	amj	…	amn
qj	q1	q2	…	qj	…	qm

Задача – выбор статистиком оптимальной стратегии.

 - решение связано с построением матрицы рисков.

Фиксируем П_j,  - максимальный выигрыш при П_j, мера благоприятности для статистика j-го состояния природы.

 - риск статистика при использовании стратегии x_i в условиях П_j.

9.2. Статистические игры без экспериментов.

9.2.1. Известны априорные вероятности состояний природы.

, .

Эксперимент недопустим  оптимизация в среднем.

 - средний выигрыш статистика для стратегии x_i.

 - максимальный средний выигрыш статистика.

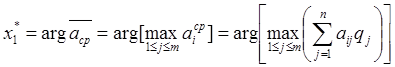 - байесовская стратегия.

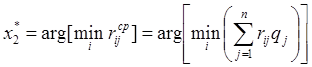 - минимизация риска.

Теорема. .

Есть смысл в смешанных стратегиях?

Пусть используется смешанная стратегия , тогда средний выигрыш , осредненный по состояниям природы, будет равен

, следовательно, , т.е. нет смысла в использовании смешанных стратегий.

9.2.2. Априорные вероятности не известны, но возможно выдвижение гипотез.

 - не известна, однако на основании опыта статистик обладает некоторыми интуитивными представлениями о том, какие состояния природы являются более правдоподобными, а какие – менее.

·   - принцип недостаточного основания Лапласа.

·   можно упорядочить в порядке убывания; ; учитывая ,  получим .

·  Проведение экспертного опроса для оценки .

9.2.3. Информация о состояниях природы отсутствует.

Может использоваться только .

·  Минимаксный критерий Вальда (хуже быть не может):

 - критерий крайнего пессимизма.

·  Минимаксный риск Сэвиджа (минимум риска):

.

·  Пессимизм-оптимизм Гурвица:

, .

При  - критерий крайнего пессимизма, при  - критерий крайнего оптимизма.

9.3. Статистические игры с экспериментом.

Эксперимент, затраты на эксперимент, снижение неопределенности природы, планирование эксперимента.

Единичный эксперимент: нет возможности менять программу эксперимента.

Идеальный единичный эксперимент: ликвидирует неопределенность природы.

Неидеальный единичный эксперимент: дополнительные сведения в пользу тех или иных состояний природы.

Последовательный эксперимент: решение о прекращении после каждого цикла.

9.3.1. Статистические игры с единичным идеальным экспериментом.

, , 

 - вероятности состояний природы, .

 - матрица выигрышей.

C – стоимость эксперимента с полным выяснением состояния природы.

Задача:  -     целесообразно ли проведение эксперимента?

-  оптимальная стратегия при проведении эксперимента или отказе от него?

Средний выигрыш  для стратегии :

.

 - оптимальная стратегия без проведения эксперимента.

Провели эксперимент , ,  - достигаемый выигрыш.