Методические указания к практическим занятиям по дисциплине «Методы и алгоритмы принятия решений», страница 20

Эксперимент целесообразен?

 - средний выигрыш без эксперимента.

 - средний выигрыш с экспериментом.

Эксперимент целесообразен  .

Т.к. , то .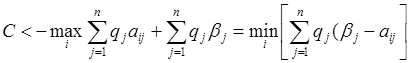

  .

Минимальный средний риск: .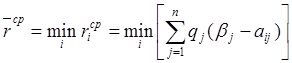

Следовательно, эксперимент целесообразен, когда .

9.3.2. Статистические игры с единичным неидеальным экспериментом.

 - полная система исходов эксперимента (исход эксперимента случаен и состоит в появлении одного из данных несовместимых событий).

, , ,  - условная вероятность исхода  эксперимента в условиях природы ; , .

ЗПР: ; ; , , , , ; С.

Задача:  -     целесообразно ли проведение эксперимента?

-  оптимальная стратегия при проведении эксперимента или отказе от него?

 - исход, который появился после реализации эксперимента.

 - апостериорные вероятности состояний природы .

Формула Байеса: .

Условный средний выигрыш статистика от стратегии x_i при условии, что эксперимент дал исход : .

Оптимальная стратегия:  

при исходе .

 - вероятность появления исхода : .

Формула полной вероятности: .

Среднее значения максимального выигрыша при проведении эксперимента:

.

Максимальный средний выигрыш без эксперимента:

.

  эксперимент целесообразен.

 - решающее правило выбора  при каждом из возможных исходов  эксперимента .

Поясним понятие решающей функции на примере. Предположим, что в некоторой задаче пространство стратегий состоит из трех элементов, т.е. , а пространство исходов эксперимента – из пяти, т.е. . Решающую функцию  можно задать в виде множества пар индексов , определяющих номер стратегии  при исходе эксперимента . Решающей функцией может быть, например, множество . Совокупность всевозможных решающих функций образует пространство  решающих функций, каждое из которых соответствует своей ЗПР.

Оптимальное байесовское решающее правило: .

Задачи к практическим занятиям.

1.  Правила парной антагонистической игры:

Первый ход – личный: 1-й игрок выбирает одно из двух чисел 1 или 2.

Второй ход – случайный: бросается монета и, если выпадает орел (и только в этом случае), сообщается 2-му игроку о выборе 1-го игрока в первом ходе.

Третий ход – личный: 2-й игрок выбирает одно из двух чисел 3 или 4.

Четвертый ход – случайный: выбирается случайным образом с вероятностями 0,4; 0,2; 0,4 одно из трех чисел -  1, 2, 3.

После 4-х ходов игра заканчивается. Результат игры: числа, выбранные в 1-м, 3-м и 4-м ходах, складываются, и полученная сумма выплачивается 2-м игроком 1-му, если она нечетная, и 1-м игроком 2-му, если она четная.

Дать формальное описание игры: .

2.  Предприятию А требуется приобрести запас черного красителя  для  тканей,  потребность в котором зависит от конъюнктурырынка (игрок В) в течение предстоящего сезона.  Эта  потребностьможет составить 10 т при пониженном спросе на черные ткани. Ценакрасителя в момент принятия решения составляет  10  тыс.руб.  затонну,  что  соответствует  пониженному  спросу.  При нормальом спросе цена красителя поднимается до 15 тас.руб., а при повышенном - до 20 тыс.руб. за тонну. Принять решение за игрока А.

3.  А - командир воинской части,  который должен  атаковатьодно из  двух  оборонительных  сооружений противника - игрока В.Противник может успешно оборонять лишь одно из этих  сооружений,но не оба сразу.  Известно,  что первое сооружение втрое важнее,чем второе. Как следует поступать обоим противникам?

4.  Лева,  ученик 10-го класса, готовится к опросу по литературе. Зазвонил телефон и знакомый сообщил, что Лева вызываетсяна экстренное заседание "клуба Эвариста Галуа".Вечер среди членов клуба,  пожалуй,  по крайней мере,  вдвоелучше  самого  блестящего ответа на уроке.  Правда,  если завтрапридется отвечать без должной подготовки,  то удовольствие можетбыть испорчено на величину, равную выигрышу при отличном ответе.С другой стороны, отказавшись от соблазна, он получит (в случае,если его вызовут) только вечер, проведенный за учебником литературы,  плюс моральное удовлетворение. Как его оценивает Лева намне известно.Найти за Леву оптимальную стратегию.