Динамические: методы вариационного исчисления.
· Вариационная задача:
![]()
где ![]()
![]() ,
, ![]() ,
,  ,
, ![]() , при ограничениях типа равенств:
, при ограничениях типа равенств:
![]() ,
,
![]()
и некоторых краевых условиях.
· Простейшая задача вариационного исчисления, когда t и x одномерны, ограничения отсутствуют, а граничные условия закрепленные:
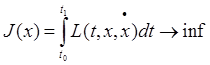 ; x(t0)=x0,
x(t1)=x1.
; x(t0)=x0,
x(t1)=x1.
К этому типу относится задача о брахистохроне или о кривой наикротчайшего спуска.
Метод ломаных Эйлера.
Интервал [t0,t1] разбивается на N
равных частей точками ![]() ,
, ![]() , …,
, …, ![]() . Значения функции в этих
точках обозначены x0, x1,
…, xN соответственно. Каждая совокупность
точек
. Значения функции в этих
точках обозначены x0, x1,
…, xN соответственно. Каждая совокупность
точек ![]() ,
, ![]() ,
…,
,
…, ![]() определяет некоторую ломаную.
Ставится задача: среди всех возможных ломаных, соединяющих точки
определяет некоторую ломаную.
Ставится задача: среди всех возможных ломаных, соединяющих точки ![]() и
и ![]() ,
найти ту, которая доставляет функционалу
,
найти ту, которая доставляет функционалу ![]() экстремальное
значение. Значение производной
экстремальное
значение. Значение производной ![]() на отрезке
на отрезке
![]() будет
будет ![]() . Функционал J(x) превращается в функцию конечного числа переменных xi:
. Функционал J(x) превращается в функцию конечного числа переменных xi: ![]() и задача
свод90ится к задаче отыскания экстремума функции
и задача
свод90ится к задаче отыскания экстремума функции ![]() .
Для того, чтобы ломаная Эйлера, реализующая экстремум этой функции,
аппроксимировала решение задачи с высокой точностью, число N
должно быть достаточно велико.
.
Для того, чтобы ломаная Эйлера, реализующая экстремум этой функции,
аппроксимировала решение задачи с высокой точностью, число N
должно быть достаточно велико.
Метод Галеркина.
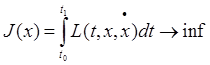 ; x(t0)=0,
x(t1)=0.
; x(t0)=0,
x(t1)=0.
Пусть разыскивается решение в
форме ![]() , где
, где ![]() некоторая система функций,
удовлетворяющая условиям
некоторая система функций,
удовлетворяющая условиям ![]() , i=1, …, N. Тогда функционал J(x) становится функцией
коэффициентов
, i=1, …, N. Тогда функционал J(x) становится функцией
коэффициентов ![]() , и задача сводится к
отысканию экстремума этой функции N переменных. При
некоторых условиях, наложенных на систему функций
, и задача сводится к
отысканию экстремума этой функции N переменных. При
некоторых условиях, наложенных на систему функций ![]() ,
решение задачи стремится при
,
решение задачи стремится при ![]() к
решению исходной задачи.
к
решению исходной задачи.
Метод вариаций.
Пусть тем или иным способом
построена функция x(t). Будет
ли эта функция решением вариационной задачи? Введем понятие вариации ![]() функционала J
для простейшей вариационной задачи
функционала J
для простейшей вариационной задачи
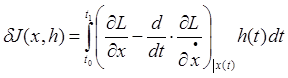 ,
где h(t) – произвольная гладкая
функция, удовлетворяющая условиям h(t0)=h(t1)=0. Условие
,
где h(t) – произвольная гладкая
функция, удовлетворяющая условиям h(t0)=h(t1)=0. Условие ![]() является необходимым, для
того, чтобы функция x(t)
реализовала экстремум функционала. Необходимым условием этого будет
удовлетворение функцией
является необходимым, для
того, чтобы функция x(t)
реализовала экстремум функционала. Необходимым условием этого будет
удовлетворение функцией ![]() дифференциальному
уравнению 2-го порядка относительно функции x(t):
дифференциальному
уравнению 2-го порядка относительно функции x(t): 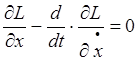 .
.
Таким образом, для решения вариационной задачи надо решить краевую задачу x(t0)=x0, x(t1)=x1 для приведенного уравнения. Получится конечное число решений. Каждую из полученных экстремалей далее необходимо подвергнуть дополнительному исследованию, чтобы определить, имеется ли среди них кривая дающая решения задачи.
· Задачи оптимального управления.
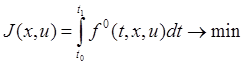
при дифференциальной связи ![]() ,
, ![]()
и граничных условиях ![]() .
.
![]() -
фазовый вектор,
-
фазовый вектор, ![]() - вектор управления,
- вектор управления,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Задачи, укладывающиеся в эту схему, имеют огромное прикладное значение. Пусть, например, уравнение описывает движение некоторого динамического объекта, например, космического корабля. Управление – вектор u – тяга его двигателя. Начальное положение – это некоторая орбита, конечное положение – это орбита другого радиуса. Функционал J описывает расход горючего на выполнение маневра. Тогда задачу применительно к данной ситуации можно сформулировать следующим образом: определить закон изменения тяги двигателя космического аппарата, совершающего переход с одной орбиты на другую за фиксированное время так, чтобы расход топлива был минимальным. При этом необходимо учитывать ограничения на управления: тяга двигателя не может превосходить некоторой величины и угол поворота тяги тоже ограничен.
Согласно принципу максимума Понтрягина, оптимальное управление u(t) должно доставлять при каждом t абсолютный максимум функции Гамильтона
![]() , где
, где ![]() определяется
системой уравнений
определяется
системой уравнений ![]() .
.
Из этого условия находится
управление ![]() и подставляется в систему
уравнений
и подставляется в систему
уравнений
![]() ,
,
![]() . В результате получается
краевая задача для 2n дифференциальных уравнений с 2n граничными условиями. Решение последней задачи реализуется
численными методами.
. В результате получается
краевая задача для 2n дифференциальных уравнений с 2n граничными условиями. Решение последней задачи реализуется
численными методами.
Задания к практическим занятиям
Найти решение задачи нелинейного программирования:
1. Минимизировать
![]() при ограничениях
при ограничениях ![]() ;
; ![]()
2. Минимизировать
![]() , ограничения
отсутствуют.
, ограничения
отсутствуют.
3. Минимизировать
Ограничения: 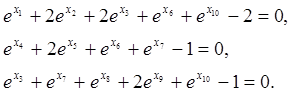
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.