Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 8

⎣ 0 ⎦

где  Z_ê = NZ_â ⋅N_t – матрица контурных сопротивлений;

           I_ê – контурный ток (ток хорд);

           M_α – матрица соединения ветвей в узлах дерева;

          N – матрица соединения ветвей в узлах контурах.

Падения напряжения узлов относительно балансирующего

U&U&âα.

Система решаемых контурных уравнений равна числу независимых контуров k = m − n +1.

3.2. Решение типовых задач

ЗАДАЧА. Для заданного варианта схемы, представленной на рисунке, параметров сети и задающих нагрузок составить в матричной форме: а) обобщенное уравнение состояния электрической цепи; б) узловое уравнение; в) контурное уравнение.

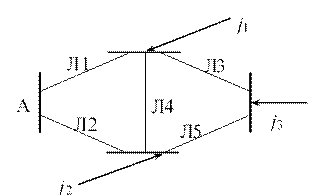Сопротивления линий (Ом):

Z₁ =1; Z₂ =1; Z₃ =1;

Z₄ = 2; Z₅ =1.

Задающие токи (А):

J₁ = −4; J₂ = −6; J₃ = −2.

Узел А принять базисным и балансирующим. Напряжение в узле А принять равным 10 В.

РЕШЕНИЕ:

Для упрощения: сопротивления линий, задающие токи узлов и напряжение в балансирующем узле принять вещественными.

Для выполнения условий а), б) и в) необходимо исходные данные представить в матричной форме, составить матрицы М и N.

Исходными данными являются сопротивления ветвей, которые представляются диагональной матрицей, а задающие токи в узлах и напряжение узла А – в виде матрицы столбца. 1

110

^Z_â =1  (Ом); J^&_i = − 6 (А);  ^U_A =^U₀ = 10 (В).

210

1

Матрицы М и N составляются по схеме замещения и графу. Составим граф схемы, где зададимся направлениями в ветвях, считая принятые направления совпадающими с направлениями токов в схеме, а также направлениями обхода контуров. Узел А принимаем в качестве балансирующего (нумерацию узлов и ветвей осуществляем по принципу ярусности).

1

                                                                                                            −1     0      1      1      0

M  =0  −1     0        −1     1;

10 4240 434−1 1420 43−1

                                                                                                                         Mα                         Mβ

                                2                            

                                                                                                                 1     −1     0     1    0

N  =

                                                                                                −114241 434−1    0{1

                                                                                                                             Nα                       Nβ

а) Обобщенное уравнение состояния электрической цепи

A⋅ I = F

                                                                          ⎡ M ⎤                 ⎡J&⎤

                                                            A = ⎢⎣NZ_â ⎥⎦;         F = ⎢⎣0⎥⎦.

Определим

                                                                                  ⎡1                        ⎤

                                                                                  ⎢     1                  ⎥

                      ⎡ 1     −1     0     1    0⎤   ⎢                      ⎥     ⎡ 1            −1       0      2    0⎤

[NZâ ]= ⎢⎣−1    1     −1   0   1⎥⎦×⎢⎢         1               ⎥⎥ = ⎢⎣−1                  1     −1   0     1⎦⎥.

2

                                                                                  ⎢                      ⎥

                                                                                 ⎢⎣                   1⎥⎦

Итак, обобщенное уравнение для заданной схемы имеет вид:

                                              ⎡−1     0      1      1       0 ⎤    ⎡I₁ ⎤      ⎡4⎤

⎢ 0 ⎢ ⎢ 0 ⎢ 1 ⎢ ⎢⎣−1

−1 0 −1 1

0 −1 0 −1

−1 0 2 0

1 ⎥     ⎢I2⎥⎥       ⎢⎢6⎥⎥        ⎥   ⎢ −1⎥×⎢I3⎥ = −⎢2⎥.        ⎥   ⎢   ⎥          ⎢ ⎥ 0  I4⎥ ⎢0⎥ ⎥   ⎢ 1  ⎥⎦  ⎢⎣I5⎥⎦  ⎢⎣0⎥⎦