Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 3

               а)                                                             б) ×            ×    ;

                                                              −1 23 0                                 5 1      5

1

                                                                                                                     2 − 4 6       5 0

                      − 2     3 4 0         0 −1

                                            в) ;                                    г) 5         2 7 × 0 2       0 ;

                             5 −1 2 3      −1

−10 0 −1

4

                        3    2 −1                      3 0 03 0 0                             2 −1

                д) 4     5                                                      е) 0 35

                        1 − 2    3                      0 0 30 0 3                      1 − 2    3

Сопоставить результаты перемножения д) и е).

Решение примера в):

                                              1     2

− 2              3 4 00 −1− 2⋅1+ 3⋅0+ 4⋅(−1) + 0⋅4            − 4 −3+ 0+ 0

= 5 −1 2 3−1 05⋅1+ (−1)⋅0+2⋅(−1) + 3⋅4 10+1+ 0+ 0

                                              4    0

−6 −7

.

                                                                     15    11

1.2.3. Даны матрицы A =[^a_ij ]_2×3; B =[^b_ij ]_3×1; C =[^c_ij ]_3×3.

Существуют ли произведения:

               а) A × B;              б) B×A;               в) A×C;               г) C×A;

                д) C×B;                е) A×B×C;          ж) A×C×B;        з) C×B×A.

Решение данного типа задач основано на знании правил умножения матриц, поэтому последовательность решения не приводится.

1.2.4. Произвести транспонирование матриц:

                                                     a11 a12 a13 a14 a151                               0− 2 2

а) A =a₂₁ a₂₂ a₂₃ a₂₄ a₂₅; б) B =−1 2 ;  в) K =3 4; a31 a32 a33 a34 a353− 2−5 −6

−1−1 4

1 2 7

                     г) C =2 −1 0 6 ;                    д) F =0 1       5 ;                 е) F =;

0  9 10

1  1 5 42 3−1

                                   1    5 6

ж) L = з) (B+ K)_t ;  и) (D×K)_t . 2 − 2 3

1.2.5. Найти матрицу обратную заданной:

1 0 11 0 01 −31 − 2 3

                   а) 0 0 2 ;              б) 0 5 0 ;             в) −3      5       6 ; г) 4       0  5 ;

                                                    −1 3 10 0 6− 2                              2 10−1          2

1 1 21 2 32 −1 11 2 3

                  д) 2 3 5 ;               е) 2 1 1 ;              ж) 1 − 2 3 ;           з) 2 3 2 ;

4 3 63 3 42 −3 21 1 4

                                         1 −32                        53 − 4                        51 3 5

                  и) 1 −8        2 ; к) 6      3    4 ;                 л) 2 −3м) 2 4

−15 − 23 −5 −18 9 7

Решение примера д):

Найти матрицу, обратную матрице A = 2 3 5 .

                                                                                           A11      A21       A

                                                                   A−1 =A12               A22       A

                                                                                          A13      A23       A

где A_ij = (−1)^{i+ j} ⋅ M _ji – алгебраическое дополнение, определенное по исходной матрице А. Вычислим detA:

detA =1⋅3⋅6−1⋅3⋅5−1⋅2⋅6− 2⋅3⋅4 + 2⋅3⋅2 +1⋅4⋅5 = −1.

Так как detA ≠ 0, то матрица А имеет обратную матрицу. Найдем алгебраические дополнения матрицы А:

3 5

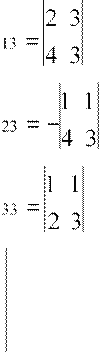
                      A₁₁ == 3;                  A₁₂ = −      = 8;                   A= −6;

3 6

1 2

               A₂₁ = −      = 0;            A₂₂ =       = −2;                    A=1;

3 6

1 2

                     A₃₁ == −1;                A₃₂ = −      = −1;                 A=1.

3 5

                                                                                            3−3                0    1

                                                         A-1 =8 − 2 −1 = −8            2     1 .