Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 19

Решая систему двух уравнений относительно ^P_max и ^P_min , получаем ^P_max =155êÂò, ^P_min = 5êÂò. Плотность распределения значений нагрузки

                                                            1                 1           1

                             p(P) =                 =           =       = 0,00666 1êÂò.

                                               Pmax − Pmin       155−5    150

1) Вероятность нахождения значений нагрузки в интервале

10 − 40 êÂò

p .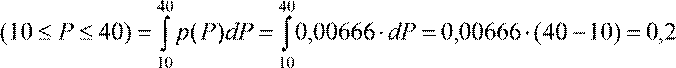

2)  Значение нагрузки P_γ, вероятность превышения которого γ = 0,05

155

∫ p(P)dP = γ = 0,05;

P_γ

0,00666⋅(155− P_γ ) = 0,05;

P_γ 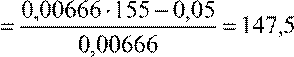 êÂò.

3)  Вероятность того, что нагрузка будет меньше 55 кВт

p .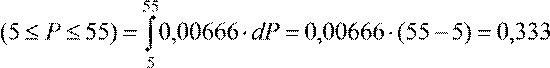

ЗАДАЧА № 2

Решить предыдущую задачу при условии, что активная мощность потребителей узла нагрузки распределена нормально с числовыми характеристиками

M(P) = 80 êÂò, σ _p = 43,3 êÂò.

РЕШЕНИЕ:

Нормально распределенная плотность вероятности нагрузки описывается уравнением 

p.

1. Вероятность нахождения значений нагрузки в интервале

10 − 40 êÂò

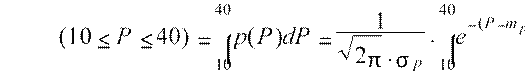p dP.

P − m_p

Пусть x = ;  dP = σ _p ⋅dx,  тогда σ _p

40−m_p

p (10 ≤ P ≤ 40) = 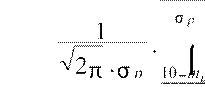²σ _p ⋅dx =

p(10 ≤ P ≤ 40) = Φ⎜    ⎟ −Φ⎜ ⎟ = ⎝  43,3 ⎠     ⎝ 43,3 ⎠      

= Φ(−0,9238) −Φ(−1,617) = 0,1236.

2. Значение нагрузки P_γ , вероятность превышения которой γ = 0,05 определяется из выражения

(P−m_p )² −

edP =

                                                 P_γ                                   P                     p

(P−m_p )²

                                                                                      P_γ                                        −

edP.

                                                                                     −∞   2π ⋅σ p

Используя, как и ранее замену переменной, получим

                                                                               ⎛ P_γ −80⎞           ⎛ P_γ −80⎞

                                     0,5 = Φ(∞) − Φ⎜⎜⎝ _43,3 ⎟_⎠⎟ =1− Φ⎜⎜_{⎝ 43,3} ⎟⎟_⎠;

⎛ P_γ −80⎞

Φ⎜⎜⎝ _43,3 ⎟⎟_⎠ = 0,95.

Находим обратную функцию Лапласа Φ' от величины 0,95

Φ'(0,95) =1,64, следовательно

P_γ −80

                                                        =1,64;     P_γ =151 êÂò.

43,3

3. Вероятность того, что нагрузка будет меньше 55 кВт:

p(−∞ ≤ P ≤ 55,0) = 55∫ p(P)dP = Φ⎜⎛55− mp ⎞⎟ = Φ⎜⎛55−80⎟⎞ =

                                                                   −∞                       ⎜⎝   σ p       ⎟⎠      ⎝    43,3 ⎠   

= Φ(−0,577) = 0,281.

ЗАДАЧА № 3

Активная мощность потребителей электроэнергии узла нагрузки распределена экспоненциально со значениями числовых характеристик M(P) = σ _p = 80 êÂò.

Определить: 

1.  Вероятность нахождения в интервале 10 − 40 êÂò.

2.  Значение нагрузки P_γ, вероятность превышения которого γ = 0,05.

3.  Вероятность того, что нагрузка будет меньше 55 кВт.

РЕШЕНИЕ:

Экспоненциальная функция распределения плотности вероятности активной мощности имеет вид

                                                            p(P) = α⋅e^−αP    (0 ≤ P ≤ ∞).

Для экспоненциального распределения M(P) = σ _p =1α, откуда α =1M(P) =180 = 0,0125 1êÂò.