Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 18

Таким образом дисперсия токов ветвей зависит не только от обобщенных параметров схемы, дисперсий токов нагрузок D(J) и дисперсий свободных ЭДС D(E), но и от вероятностной взаимосвязи между режимами электропотребления в узлах (матрица коэффициентов корреляции η_kl ), вероятностной взаимосвязи между изменениями свободных ЭДС ветвей (матрица η_pq ), вероятностной взаимосвязи между режимами электропотребления в узлах нагрузки и изменением свободных ЭДС ветвей (матрица η_kp ).

Если принять, что указанные совокупности случайных величин, входящих в систему случайных векторов, взаимнонезависимыми, то нахождение дисперсии упрощается

D(I) = C_ik² ⋅D(J) + Y_ip² ⋅D(E).

Для получения числовых интегральных характеристик напряжений узлов рассмотрим связь между напряжениями узлов и активными параметрами схемы замещения J, E .

Основное узловое уравнение

UE,

где  U_Δ =U₀ −U_y ;

          U₀ – напряжение базисного узла;

          U_y – матрица-столбец напряжений узлов;

Z  – матрица квадратная, собственных и взаимных сопротивлений схемы;

Z_y  H – матрица коэффициентов распределения напряжений.

Получаем матрицу напряжений узлов

U_y =U₀ −U_Δ =U₀ −[Z ⋅ J + H ⋅E]  –  основное уравнение связи между активными параметрами схемы замещения и напряжением узлов.

Матрица математических ожиданий напряжений узлов вычисляется по матрице математических ожиданий свободных ЭДС

M(U_y ) =U _y =U₀ − M[Z ⋅ J + H ⋅E].

Матрица дисперсий напряжений узлов

                D(U_y) = D(U₀ + Z_ik² D(J) + H D(E) + ∑Z_ik ⋅Z_il ⋅σ_Jk ⋅σ_Jl                       +

k≠l

+ ∑Hip ⋅Hiq ⋅σEp ⋅σEZik ⋅Hip ⋅σJk ⋅σEp

r≠q

⎡n

+ ⎢− ∑Z_ik ⋅σ_Jk ⋅σ_U0 ⋅ηip ⋅σEp ⋅σU0 ⋅ηU0Ep

⎢⎣k=1

где ^η_U0Jk , ^η_U0Ep – соответственно коэффициенты корреляции между случайной величины напряжения базисного узла и случайными величинами – нагрузкой k-го узла и свободной ЭДС р-ветви.

Если известны числовые интегральные характеристики параметров режима системы, то предполагая из физических соображений вид закона распределения исследуемого параметра можно, определить расчетные его X_p с заданной вероятностью превышения. Для этого необходимо решить уравнение относительно X_p , а именно

∞

∫ p(x)dx = γ ,

X _p

где p( )x – плотность распределения параметра х.

Рассмотрим следующие случаи распределения параметра режима:

–  нормальный закон – X_p = X + Φ⁻¹(1− γ)σ_x ,

                                  1     x        2

где     (                             dt – функция Лапласа;

–  экспоненциальный закон – X_p = X + σ_x [−lnγ −1];

–  равномерный закон – X_p = X + σ_x [ 3(1− 2γ)].

Вероятность нахождения параметров в диапазоне [x₁, x₂] определяются по формуле

x₂

p(x₁ ≤ x ≤ x₂) = ∫ p(x)dx.

x₁

По интегральным характеристикам нагрузок элементов сетей в них просто вычислить потери мощности и энергии.

Математическое ожидание потерь активной мощности в элементе сети трехфазного тока

M[ΔP] = M[3⋅ I ² ⋅R]= 3⋅R⋅M[I ² + D(I)].

Потери электроэнергии в элементе сети за время Т

.

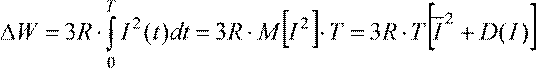6.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

ЗАДАЧА № 1 

Активная мощность потребителей электроэнергии узла нагрузки распределена равномерно в некотором диапазоне значений. Математическое ожидание и среднеквадратическое отклонение значение мощности соответственно

M(P) = 80 êÂò, σ _p = 43,3 êÂò.

Определить: 

1) Вероятность нахождения значений нагрузки в интервале

10 − 40 êÂò p (10 ≤ P ≤ 40).

2)  Значение нагрузки P_γ , вероятность превышения которого γ = 0,05.

3)  Вероятность того, что нагрузка будет меньше 55 кВт.

РЕШЕНИЕ:

Определим диапазон изменения случайной величины нагрузки. При равномерном законе распределения вероятностей случайной величины ее математическое ожидание и среднеквадратическое отклонение выражаются через границы диапазона изменения

M êÂò;

                                                                          P     − P

êÂò.