Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 20

Следовательно

p(P) = 0,0125⋅e−0,0125⋅P .

1.  Вероятность нахождения нагрузки в интервале 10 − 40 êÂò

                                                                           40                          40

  p(10 êÂò≤ P ≤ 40 êÂò) = 10∫ p(P)dP = 10∫0,0125⋅e^−0,0125ÐdP =   

= e−10⋅0,0125 − e−40⋅0,0125 = 0,88−0,606 = 0,274.

2.  Значение нагрузки P_γ, вероятность превышения которого γ = 0,05 определяется из выражения

                                                           Pγ                          Pγ

0,95 = ∫ p(P)dP = ∫0,0125⋅e^−0,0125ÐdP =

−0,0125⋅P^γ

                                               1−0,95 = e             ;  P_γ = 239,6 êÂò.

               При M(P) = σ _p = 43,3 êÂò             P_γ =129,7 êÂò.

3.  Вероятность того, что нагрузка будет меньше 55 кВт

p(0 êÂò≤ P ≤ 55êÂò) 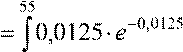^ÐdP =

                                                                                0                                                                             

= e0 − e−0,0125⋅55 =1−0,503= 0,497.

ЗАДАЧА № 4

Промышленное предприятие получает электроэнергию по двум параллельно работающим КЛ длиной 5 км, с сечением алюминиевых жил 3×240 ìì (r₀ = 0,132 Îì êì ) с U_í =10 êÂ. За год потребляет

76⋅10⁶ êÂò⋅÷ электроэнергии.

По замерам в период максимума и минимума нагрузок получены практически максимально и минимально возможные их среднечасовые значения 

                                                          I_max = 460 A;       I_min = 40 A.

Определить потери электроэнергии за год в КЛ, полагая, что значения нагрузки предприятия распределены по нормальному закону.

Принять cosϕ_í =1.

РЕШЕНИЕ:

Потери электроэнергии в элементе трехфазной сети переменного тока вычисляются по формуле

ΔW = 3⋅R⋅T([M(I)]² + D(I))= 3⋅R⋅T[[I ² + D(I)]].

Для нахождения потерь энергии за год необходимо знать среднегодовое значение тока и его дисперсию. Среднегодовое значение тока

                                T                              Ý                           76⋅10⁶

      I =                       =                           =                      = 250,4 A.

                      3⋅U_í cosϕ⋅n      Ò⋅    3⋅U_í cosϕ⋅n      8760⋅   3⋅10⋅1⋅2

При нормальном законе распределения случайной величины вероятность нахождения ее значений в диапазоне

(I − 3⋅σ_I ≤ I ≤ I + 3⋅σ_I ) равна 0,0027 (правило трех сигм).

Поэтому для практических инженерных расчетов можно принять, что

                                              Imax = I + 3⋅σI ;              Imin = I −3⋅σI .

I^max − I^min = 460− 40 = 70 (À). Следовательно, σ_I =

                                                                                    6                  6

Потери электроэнергии в кабельных линиях за год

ΔW = 3⋅0,132⋅5⋅8760⋅(250,4² + 70² )⋅10⁻³ ⋅2 = 234,6⋅10⁴ êÂò⋅÷, что составляет 3,08 % от передаваемой энергии.

Сравним полученный результат с результатом расчета по общепринятому методу – по времени потерь τ

                                                                  2                                                               2

⎛ T^{íá ⎞} ⋅8760 = ^⎛_⎜0,124 + ^{4770 ⎞}_⎟ ⋅8760 = 3164 ÷. τ = ⎜0,124 + _⎟

                         ⎝            10000⎠              ⎝            10000⎠

                                     Ý                 76⋅10⁶

где  T_íá =               =                         = 4770 ÷;

                              P_max ⋅n     460⋅   3⋅10⋅1⋅2

ΔW = 2⋅3⋅460² ⋅0,132⋅5⋅3164⋅10⁻³ = 265,08⋅10⁴ êÂò⋅÷ или 3,5 % от передаваемой мощности.

Метод, предусматривающий моделирование нагрузки случайной величиной, позволяет вычислить потери электроэнергии в схемах любых конфигураций, в т. ч. и сложнозамкнутых, по токовым числовым характеристикам нагрузок ветвей, которые рассчитываются с использованием обобщенных параметров схем замещения.

ЗАДАЧА № 5