Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 16

Как видно из таблицы итерационный процесс сошелся на 34 шаге.

Запишем полученный результат:

−5,666

U_Δ =−6,333.

−6,999

Результаты определения U_iΔ совпадают с расчетами на основе других методов, полученных ранее.

5.3. Индивидуальные задания

Для нахождения значений U_iΔ используем метод ускоренной итерации при нахождении элемента U_nΔ на шаге (k), в формулу будем подставлять найденные значения U_(n−1)Δ на этом же шаге (k), а вместо неизвестных U_n−1 – значения с предыдущего шага (k −1), тогда получим:

U; U; U.

Задаем начальные приближения:  и точность ε_i = 0,001.

Итерационный процесс проводим до того момента, пока две соседние строки не сойдутся (значения станут одинаковыми) с заданной точностью (в нашем случае до третьего знака после запятой).

Таблица

№ итерации	U1Δ	U2Δ	U3Δ
1	-1,6	-2,72	-3,16
2	-3,408	-4,3456	-4,8768
3	-4,41984	-5,23469	-5,82726
4	-4,97784	-5,72647	-6,35216
5	-5,28616	-5,9981	-6,64213
…	…	…	…
16	-5,66611	-6,33284	-6,99948
17	-5,66636	-6,33306	-6,99971
18	-5,6665	-6,33318	-6,99984

Как видно из таблицы итерационный процесс сошелся на 18 шаге.

Запишем получившейся результат:

−5,666

U_Δ =−6,333.

−6,999

Результаты U_iΔ совпадают с расчетами на основе простой итерации.

Матричное контурное уравнение итерационными методами вида

−1

M^α

                                                               Z_k ⋅ I_k = −N ⋅ Z ⋅        ⋅ J

0

с учетом исходных данных получено в теме № 3

4 − 2 I_k1 0 × = .

                                                                      − 2     4       I_k2         2

Перемножив Z_k ⋅ I_k, получим:

4⋅ Ik1 − 2⋅ Ik2 0 = .

                                                                  − 2⋅ Ik1        4⋅ Ik2           2

Из каждой системы выражаем соответствующий диагональный элемент:

4⋅ ^I_k1 = 0−(−2⋅ ^I_k2);

4⋅ ^I_k2 = 2 −(−2⋅ ^I_k1).

Теперь произведем преобразования и из каждой строки системы выразим соответствующий элемент I_ki :

I_k;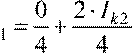

I_k.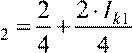

Упростим получившиеся уравнения:

Ik1 = 0,5⋅ Ik2;

Ik2 = 0,5+ 0,5⋅ Ik1.

Таким образом, мы выразили неизвестные элементы системы через другие неизвестные.

Для нахождения значений I_ki используем метод простой итерации. То есть при нахождении элемента I_ki на шаге (k), в формуле будем подставлять найденные значения I_k на предыдущем шаге (k −1), тогда получим:

I;

I.

Задаемся начальным приближением:  и точность ε_i = 0,001.

Итерационный процесс проводим до того момента, пока две соседние строки не сойдутся (значения станут одинаковыми) до заданной точности (в нашем случае до третьего знака после запятой).

Таблица

Результаты итерационного процесса

№ итерации	Ik1	Ik2
1	0	0,5
2	0,25	0,5
3	0,25	0,625
4	0,3125	0,625
5	0,3125	0,65625
6	0,328125	0,65625
7	0,328125	0,664063
8	0,332031	0,664063
9	0,332031	0,666016
10	0,333008	0,666016
11	0,333008	0,666504

Как видно из таблицы итерационный процесс сошелся на 11-ом шаге. Запишем получившейся результат: 0,333