Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 15

(k) a(n−1)1 (k) a(n−1)(n−2) (k) a(n−1)n (k−1) bn−1 ;⎪ ^x_n−1 = ₋ ^x₁ −...₋ ^x_{n−2 −} ^x_{n +}

^a(n−1)(n−1)   ^a(n−1)(n−1)       ^a(n−1)(n−1)       ^a(n−1)(n−1) ⎪ ⎪

^x_n(k) = − an1 ^x₁(k) − an2 ^x₂(k) −...− ^an(n−1) ^x_n(k₋)₁ + bn ;     ⎪ ann    ann       ann         ann       ⎪⎭

(5.7)

Достаточные условия сходимости метода простой итерации являются достаточными и для метода Зейделя. При одинаковых начальных приближениях неизвестных и одинаковой заданной точности решение по методу Зейделя получается за меньшее число итераций.

Характеризуя итерационные методы в целом, необходимо указать, что они обладают свойством самоисправляемости: любое ошибочно найденное решение может восприниматься как новое начальное решение.

Пример выполнения расчетов на ПЭВМ

Матричное узловое уравнение получено в теме № 3:

Y_y ⋅U_Δ = J ;

                                                           2,5     −0,5    −1

                                                         −0,5     2,5

                                                            −1       −1      2

перемножив Y_y ⋅U_Δ , получим

                                                2,5⋅U1Δ       −0,5⋅U_2Δ     −1⋅U3Δ

                                              −0,5⋅U_1Δ       2,5⋅U2Δ       −1⋅U3Δ

                                                 −1⋅U1Δ          −1⋅U2Δ         2⋅U3Δ

Из каждой строки системы выражаем соответствующий диагональный элемент:

2,5⋅^U_1Δ = −4 −(−0,5⋅^U_2Δ ) −(−1⋅^U_3Δ );

2,5⋅^U_2Δ = −6−(−0,5⋅^U_1Δ ) −(−1⋅^U_3Δ );

2⋅^U_3Δ = −2 −(−1⋅^U_1Δ ) −(−1⋅^U_2Δ ).

Теперь произведем преобразования и из каждой строки системы выразим соответствующий элемент U_i :

U;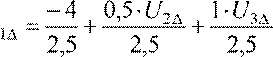

U ;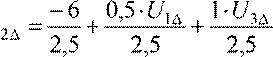

U .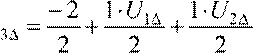

Упростим получившиеся уравнения:

U1Δ = −1,6+ 0,2⋅U2Δ + 0,4⋅U3Δ ;

U2Δ = −2,4 + 0,2⋅U1Δ + 0,4⋅U3Δ ;

U3Δ = −1+ 0,5⋅U1Δ + 0,5⋅U2Δ .

Таким образом, мы выразили неизвестные элементы системы через другие неизвестные (привели к виду (5.2).

Для нахождения значений U_iΔ используем метод простой итерации, при нахождении элемента U_iΔ на шаге (k), в формуле будем подставлять вместо неизвестных элементов найденные значения на предыдущем шаге (k −1), тогда получим:

U; U; U.

Задаем начальные приближения:  и точность ε_i = 0,001.

Итерационный процесс проводим до того момента, пока две соседние строки не сойдутся (значения станут одинаковыми) с заданной точностью (в нашем случае до третьего знака после запятой).

Таблица Результаты итерационного процесса

№ итерации	U1Δ	U2Δ	U3Δ
1	-1,6	-2,4	-1
2	-2,48	-3,12	-3
3	-3,424	-4,096	-3,8
4	-3,9392	-4,6048	4,76
5	-4,42496	-5,09184	-5,272
…	…	…	…
16	-5,62062	-6,28728	-6,93785
17	-5,6326	-6,29926	-6,95395
18	-5,644143	-6,3081	-6,96593
19	-5,64799	-6,31466	-6,97477
20	-5,65284	-6,3195	-6,98133
…	…	…	…
31	-5,66616	-6,33283	-6,99932
32	-5,66629	-6,33296	-6,99949
33	-5,66639	-6,33306	-6,99963
34	-5,66646	-6,33313	-6,99972