Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 21

От шин низшего напряжения районной понизительной подстанции получают электроэнергию четыре типа потребителей. Законы распределения случайных величин их нагрузок нормальные со следующими параметрами:

M(P1) =10;	σP1 = 3;       МВт;
M(P2) =15;	σP2 = 8; МВт;
M(P3) =12;	σP3 = 5;       МВт;
M(P4) = 20;	σP4 =10. МВт.

Вероятностные взаимосвязи между режимами электропотребления характеризуются коэффициентами корреляции

                                                                              1    0,3    0,45    0,7

                                                                                         1     −0,4    0,6

.

                                                                                                        1       0,8

1

Определить значение нагрузки на шинах подстанции, вероятность превышения которой γ = 0,05, а также коэффициент одновременности, соответствующий этой вероятности.

РЕШЕНИЕ:

Нагрузка на шинах подстанции равна сумме нагрузок отдельных потребителей. При сложении случайных величин с нормальными законами распределения в результате также получается нормальный закон. Определим числовые характеристики суммарной нагрузки 

M ìÂò .

i=1

4

D(P_Σ) = ∑D(P_i ) + 2⋅∑σ_Pi ⋅σ_Pj ⋅η_ij =

                             i=1                           i< j

                       = 3² +8² +5² +10² + 2(3⋅8⋅0,3+ 3⋅5⋅0,45+ 3⋅10⋅0,7 −         

−8⋅5⋅0,4 +8⋅10⋅0,6+5⋅10⋅0,8) =198+ 2⋅106,95 = 411,9 ìÂò.

Среднеквадратическое отклонение

                                                    σ_P = D(P_Σ) =    411,9 = 20,3ìÂò .

Значение нагрузки, вероятность превышения которой γ , вычислим из уравнения относительно P_γ в виде 

∞                                                                              Pγ Pγ edP =

                                                                                                              p             −∞

⎡P_γ − M(P)⎤

                         =1−Φ⎢ ⎥;

                                         ⎣      σ p          ⎦

P_γ = M(P_Σ ) + σ _pΦ⁻¹(1− γ);

P_γ = 57 + 20,3⋅Φ⁻¹(0,95) = 57 +1,65⋅20,3= 90,5 ÌÂò .

Коэффициенты одновременности по определению – отношение суммарной нагрузки с заданной вероятностью превышения к арифметической сумме нагрузок отдельных потребителей с той же вероятностью превышения

n

K

.

ЗАДАЧА № 6

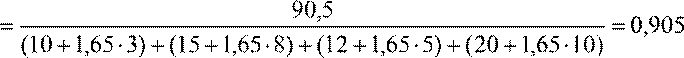Потребители пунктов П1-П3 получают электроэнергию от двух источников питания ИП1 и ИП2, напряжения на которых являются случайными величинами с числовыми характеристиками M(^U₁) =10,3 êÂ, σ_U1 = 0,05êÂ, M(^U₂) =10,1êÂ, σ_U2 = 0,03êÂ. Вероятностная взаимосвязь между режимами изменения напряжений на источниках характеризуется коэффициентом корреляции η_U1U2 = 0,6.

 ИП1 ИП2

                                                                     П1                  П2                 П3                         

Система случайных величин нагрузок потребителей имеет числовые характеристики.

                                    100                                       501                 0,3    −0,6

                       J _í = 150 ;                            σ _jí = 80 ;  1                        0,8.

                                    200                                              1001

Случайные величины нагрузок потребителей не зависят от случайных величин напряжений на ИП1 и ИП2. Сеть выполнена КЛ, активные сопротивления участков линий R₁ =1,0 Îì , R₂ = 0,5Îì , ^R₃ =1,0 Îì , ^R₂ =1,5Îì .

Определить: 

1)  расчетные максимальные нагрузки участков линий, вероятность превышения которых γ = 0,00135; 

2)  математическое ожидание потерь мощности и энергии в сети за год. Законы распределения нагрузок линии принять нормальными.

РЕШЕНИЕ:

Приведем расчетную схему замещения и вычислим числовые характеристики ЭДС контура

E = M(U₁) − M(U₂) =10,3−10,1= 0,2 êÂ.

=

Обобщенные параметры схемы: