Числовые матрицы и их преобразования. Операция сложения над матрицами. Тождества перемножения матриц, страница 6

Совокупность n ветвей схемы, составляющих минимальный связный подграф, обеспечивающий связь БУ со всеми n независимыми узлами схемы, образуют так называемое дерево сети.

3.  Когда в ходе нумерации встречается ветвь, подтекающая к ранее пронумерованному узлу, то эта ветвь замыкает собой контур – такая ветвь называется хордой. Для каждой из хорд за положительное также принимается направление от начальной вершины к конечной. Хорды условно помечаются на схеме и отдельно нумеруются (I, II, III, …, k, где k – число контуров) в дополнение к сквозной нумерации ветвей.

4.  В результате нумерации схемы формируется массив номеров узлов – из n элементов, массив номеров ветвей дерева также из n элементов и массив номеров хорд схемы – k элементов, где k + n = m – полному числу ветвей схемы.

В результате применения принципа ярусности матрицы M и N могут быть представлены блоками, относящимися к дереву схемы и хордам

                                                         M =[M_αM_β],      N =[N_αN ]_β , где  M_α, N_α – подматрицы, относящиеся к дереву схемы;

M_β, N_β – подматрицы, характеризующие подграфы, состоящие из хорд.

2.2. Решение типовых задач

ЗАДАЧА 1. Для схемы (рис. 2.3) составить направленный граф, сформировать первую и вторую матрицу инциденций для представления и анализа установившегося режима.

РЕШЕНИЕ:

Для составления направленного графа необходимо пронумеровать и задать направления в ветвях схемы замещения. Схема замещения может быть представлена с учетом схем замещения отдельных элементов следующим образом (рис. 2.4, 2.5)

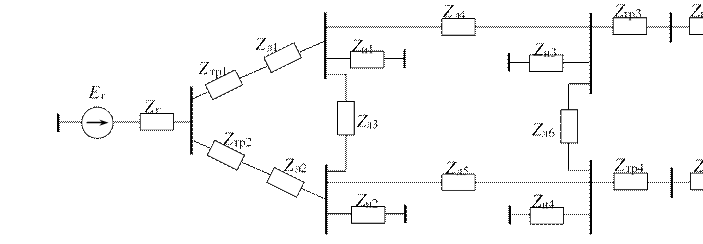
Рис. 2.4

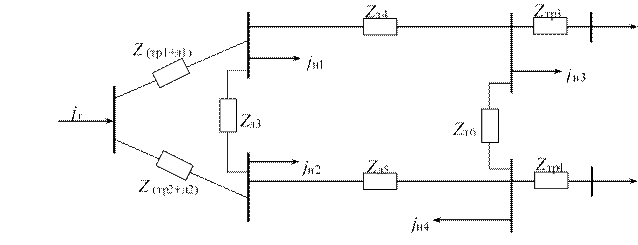
Рис. 2.5

Узлом в схеме будем считать точку, в которой объединяются две и более ветвей.

Нумерацию узлов и ветвей выполним с учетом ярусности.

Направленный граф для схемы замещения (рис. 2.5) будет

где j₃^' , j₄^' – нагрузки узлов 3, 4 с учетом нагрузок за трансформаторами.

Полная (суммарная) матрица соединений ветвей в узлах будет

5×6

-1   0   1   0  1  0

0  -1   0   1  -1  0

M_Σ =0   0  -1   0   0  1.

0  0   0  -1   0  -1

1  1   0    0  0   0

При решении установившихся режимов используется первая матрица инциденций – М, составленная без балансирующего узла, т. е. в матрице M_Σ вычеркивается строка, соответствующая балансирующему. В нашем случае в качестве балансирующего принят узел 5, поэтому матрица М будет иметь следующий вид:

-1   0   0   0  1  0

0  -1   0   0  -1  0

M  =.

0  0  -1   0   0  1

0  0   0  -1   0  -1

Для составления второй матрицы инциденций (соединение ветвей в независимые контуры) задаемся направлениями в контурах с учетом принципа ярусности, т. к. при отбрасывании двух последних ветвей мы получим схему  разомкнутой сети. Число ветвей, обеспечивающее размыкание всех контуров определяет число независимых контуров (в нашем случае – два).

1  −1 0      0 1 0

N  =.

1  −1 1 −1 0 1

Необходимо отметить, что матрицы М и N для заданной схемы могут быть другими, если отступить от принципа ярусности.

Матрицы М и N, преобразованные в блоки для нашей схемы:

-1   0   0   0  1  0

0  -1   0   0  -1  0

M  =0   0  -1   0   0  1⁼ [M_αM_β];

01   420   043  -1   0{  -1

                                                                             α                  β

                                                                  1 −1 0       0 1 0

N  =11−421 143−1 0{1⁼ [N_αN_β].

                                                                              α                 β

2.3. Варианты индивидуальных заданий

Принять по таблице П1 и схемам, приведенным в Приложении.

3. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ СЕТИ В МАТРИЧНОЙ ФОРМЕ

3.1. Теоретическая часть

Задачей расчета установившегося режима электрической системы является определение токов в ветвях схемы замещения, напряжений в ее узловых точках, мощностей. В общем случае замкнутой схемы замещения задача решается одним из следующих путей: