Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 7

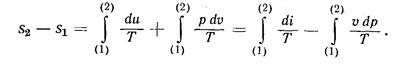
Последние два уравнения позволяют определить изменение энтропии в зависимости от изменения параметров в любом термодинамическом процессе.

Выше рассмотрены обратимые термодинамические процессы, допускающие возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Условием обратимости процесса является его равновесие.

Все реальные процессы протекают с конечной скоростью. Они сопровождаются потерями механической и тепловой энергии вследствие, например, трения поршня о стенки цилиндра и теплообмена между системой и внешней средой. Такие процессы называют необратимыми. Чтобы вернуть такую систему в первоначальное состояние, нужно в окружающую среду внести соответствующие изменения.

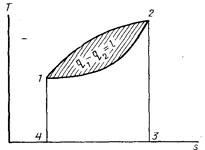  Рис. 4. Изображение кругового цикла в координатах Ts

Для любого необратимого цикла уравнение (1.8) остается справедливым, однако выражение (1.8а) не выполняется, так как вследствие потерь теплоты термический к. п. д. Необратимого цикла меньше к. п. д. обратимого. Тогда

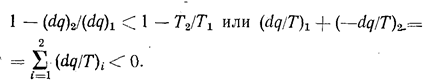
Выполняя предельный переход, получаем:

Для необратимого цикла равенство ds = dq/Т не выполняется. Чтобы показать это, рассмотрим необратимый цикл, состоящий из необратимого процесса А от состояния (1) до состояния (2) и обратимого процесса В от состояния (2) до состояния (1). Для необратимого цикла в соответствии с (1.12) получим:

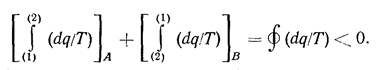
Для обратимого процесса В в соответствии с (1.10а):

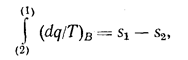
тогда

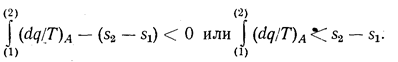
Отсюда следует, что в необратимом цикле ds > dq/T, т. е. энтропия увеличивается (Ds>0).  В общем виде можно записать, что Ds ³ 0. Все реальные процессы являются необратимыми, поэтому энтропия изолированной системы увеличивается. Чем больше изменение энтропии ds, тем более неравновесно состояние термодинамической системы. Величина изменения энтропии может служить мерой вероятности наступления равновесного состояния системы. Больцманом было доказано, что равновесное состояние системы является наиболее вероятным. Поэтому любое неравновесное состояние будет переходить в равновесное, характеризуемое своими  параметрами состояния. Переход системы в равновесное состояние сопровождается увеличением энтропии системы. С увеличением энтропии в необратимых процессах преобразование энергии системы в работу осложняется. В равновесной системе преобразование энергии в работу вообще невозможно. В связи с этим существует иная формулировка второго закона термодинамики, утверждающая невозможность совершения работы за счет энергии тел, находящихся в термодинамическом равновесии.

Физик Клаузиус рассматривал Вселенную как замкнутую неравновесную термодинамическую систему. В результате протекающих в ней необратимых процессов энтропия Вселенной все время должна расти с одновременным сокращением обмена энергией. После достижения Вселенной состояния равновесия ее энтропия достигнет максимума, процессы обмена энергией прекратятся, и наступит тепловая смерть. Теория тепловой смерти базируется на неправомерном распространении выводов термодинамики изолированных систем на Вселенную.

15. Максимальная работа. Эксергия

Рассмотрим изолированную систему, состоящую из рабочего тела и окружающей среды. Система может совершать работу, если она находится в неравновесном состоянии. Для получения возможной работы при переходе системы в равновесное состояние нужно, чтобы все процессы, протекающие в системе, были обратимыми.

Параметры рабочего тела Р, Т, а среды соответственно Р₀ и Т₀, причем Р ¹ Р₀, а Т ¹ T₀. Внутренняя энергия и объем рабочего тела в начальном неравновесном состоянии равны U₁ и V₁. Эти же параметры в состоянии равновесия обозначим U₂  и V₂. Начальная внутренняя энергия среды U₀₁  а конечная U₀₂.

Суммарная внутренняя энергия при неравновесном состоянии системы U¢_с = U₁ + U₀₁ , а в конечном равновесном состоянии U¢¢_с = U₂ + U₀₂.