Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 32

Построение явной формы баланса энтропии для конкретных термодинамических систем достигается подстановкой законов сохранения (1.2)—(1.5) в соотношение Гиббса в формах (l.la), (1.1). Последующее сравнение результата с (1.6) определяет явный вид выражений потока и производства энтропии.

Так, для непрерывных систем (1.13), (1.14)

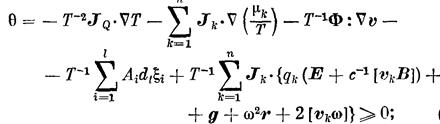
для прерывных систем (1.15), (1.16)

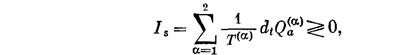
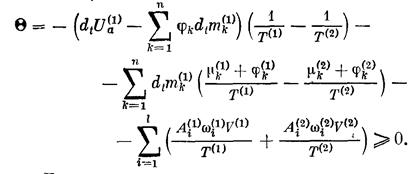
8.2. Основы теории Онсагера

Классическая  термодинамика  не  в  состоянии  предсказать  поведение  термодинамических систем в неравновесных превращениях, например предсказать скорость протекания этих процессов. В качестве необратимых процессов можно рассматривать такие процессы, как  теплопроводность, электропроводность, диффузия и некоторые другие. Эти  процессы необратимы  по своей  природе, так как  протекают  под  воздействием конечных  разностей потенциалов:  температуры, электрического потенциала, концентрации и т. д.                                                           

Если исключить из рассмотрения такие крайние случаи, как перенос под  воздействием больших градиентов температур и концентраций,  для которых  применение понятий  температуры, энтропии и т. п. сомнительно, то, как показывает  опыт, названные  выше процессы  подчиняются линейным феноменологическим законам переноса градиентного типа. Для  теплопроводности это  закон Фурье

(14.54)

где q- плотность теплового потока; - теплопроводность; Т - температура;                  

Для электропроводности - закон Ома                                                      

(14.55)

где  J - поток электрического заряда;  - злектрический потенциал;- электропроводность.

И наконец, для описания процессов диффузии используется закон Фика                       

 (14.56)

где  J_i- поток  массы  i-го компонента; D_ik- диффузия i-го компонента относительно k-го компонента; C_i- массовая концентрация i-го компонента.                                          

Эти законы, полученные на основе опыта, носят название ф е но м е н о л о г и ч е с к и х .

Теперь предположим, что два или несколько явлений  переноса происходят  одновременно. Известно, что в результате взаимодействия этих явлений могут возникать новые физические явления.

Так  например,  взаимодействие  теплопроводности  и  электропроводности в цепи, составленной из двух  однородных  (но  различных)  проводников электричества,  спаи которых  поддерживаются при различных  температурах,   сопровождается  двумя   термоэлектрическими  эффектами:   эффектом  Зеебека и эффектом  Пельтье. Другой  пример:  взаимодействие  процессов теплопроводности диффузии в газах приводит к термической диффузии, т. е.  возникает поток  массы вещества  под действием градиента температуры.                                                                       

Математически   эти   эффекты   учитываются   добавлением    новых   членов    в   феноменологические законы  переноса.  Так,  например,  если  через J₁ и J₂ обозначить  потоки  теплоты  и вещества,  а через  X₁ и  Х₂ градиенты  температуры  и  концентрации,  которые  в  дальнейшем  мы  будем  называть  д в и ж у щ и м и с и л а  м и  или  сокращенно  с и л а м и, то  феноменологические законы  принимают вид

                                       (14.57)

где коэффициенты L₁₁,L₁₂,… называются феноменологическими (или кинетическими).                          

В настоящее время статистическая и кинетическая теории газов в состоянии предсказать числовые значения этих коэффициентов. Вместе с тем, как будет  показано ниже,  термодинамика необратимых процессов  вне зависимости  от особенностей  молекулярного строения  вещества также в состоянии указать методы вычисления этих коэффициентов.                                                  

Как было показано выше  [см. (14.54)  - (14,56)  ], силы  Х_i  являются  первопричиной  возникновения  необратимых  процессов  переноса.  В  общем  случае  можно  записать   уравнений  в виде