Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 31

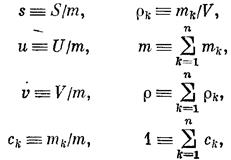
где s, и, v — удельные энтропия, внутренняя энергия и объем; т_k,r_k, c_k — масса, плотность и массовая концентрация (доля) k-ro компонента системы; т, r — общие масса и плотность системы.

При наличии в системе химических реакций (релаксационных процессов) соотношение Гиббса и формах (1.1), (l.la) необходимо дополнить. Пусть и каждой точке системы осуществляется I химических реакций в соответствии с уравнениями

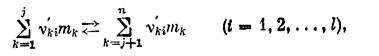
где n¢_ki — стехиометрический коэффициент k-го компонента системы в 1-й реакции. Причем, по определению, коэффициент n¢_ki  положителен, если находится в правой части уравнения (k= j + 1, …l), и отрицателен, если находится в левой части (k = 1, 2, . . ., j). В каждой i-й реакции выполняется закон сохранения массы

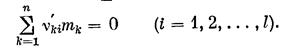
В этой связи целесообразно ввести новые стехиометричеcкие коэффициенты

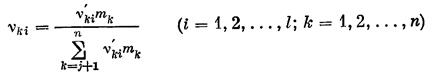
и переписать закон сохранения массы для отдельной реакции в форме

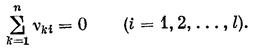
Одновременно новые коэффициенты n¢_ki упрощают запись локальных скоростей химических реакций в непрерывной системе. Так, если w_i º r¶_ix_i º rx_i — скорость i-й химической реакции, имеющая размерность массы на единицу объема в единицу времени, а 0 £ x_i £1 — степень завершенности (полноты) i-й химической реакции (релаксационного процесса), то справедливы следующие соотношения:

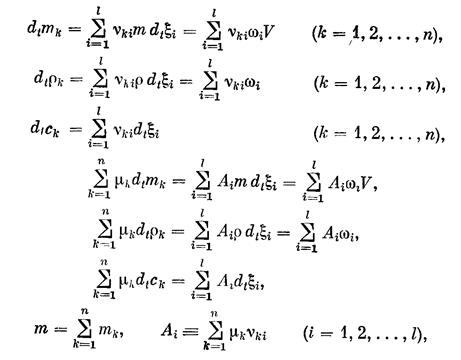
где Ai — сродство t-й химической реакции (релаксационного процесса).

В духе принципа локального равновесия термодинамику необратимых процессов можно рассматривать как полевую теорию и формулировать для нее законы сохранения. При этом целесообразно выделить два класса термодинамических систем — непрерывные и прерывные (вентильные). К первому классу относятся системы, в которых переменные, определяющие их состояние, являются непрерывными функциями пространственных координат и времени. Второй класс включает системы, состоящие из двух и более подсистем, разделенных естественной или искусственной границей. Параметры состояния каждой подсистемы зависят только от времени (идеальное перемешивание) и при переходе от одной подсистемы к другой меняются скачком.

Для непрерывных систем законы сохранения, представленные в локальной и субстанциональной формах, имеют вид следующих балансных соотношений.

Баланс массы: (1.2)

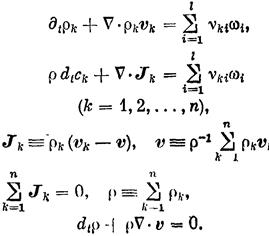
Баланс заряда (1.3)

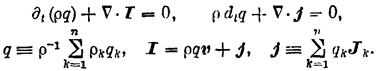
Баланс импульса: (1.4)

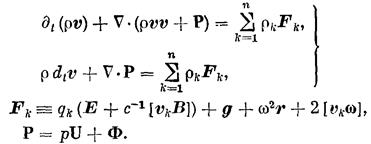
Баланс полного момента количества движения: (1.4а)

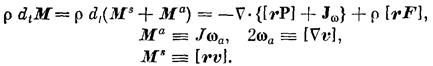
Баланс внутренней энергии: (1.5)

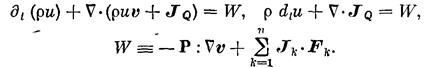
Баланс энтропии:    (1.6)

в этих выражениях q_k, v_k, J_k- заряд единицы массы, скорость и диффузионный поток k-го компонента системы;q - полный заряд единицы массы; J_Q, J_s - потоки тепла и энтропии; v - скорость центра масс; Р - вязкий тензор давления; р — давление; U - единичный тензор; Ф - тензор давления; F_k - вектор внешних сил, действующих на единицу массы k-го компонента системы; j, I - диффузионный и полный электрические токи; g- гравитационное   ускорение;   r — радиус-вектор; w— угловая скорость вращения системы; E — вектор напряженности электрического поля; В — вектор магнитной индукции; М - полный момент количества движения единицы массы системы; M^s, М^a — внешний и внутренний моменты количества движения единицы массы системы; J — средний момент инерции частиц, образующих единицу массы системы; w_a — угловая скорость внутреннего вращения элемента объема системы; J_w, — аксиальный вектор (антисимметричный тензор) плотности потока внутреннего момента количества движения;

W — источник внутренней энергии; q— локальное производство энтропии; ¶_t — оператор частной производной по времени t.

Центральное место среди этих соотношений занимает уравнение баланса энтропии в форме (1.6), разделяющее изменения энтропии за счет взаимодействия системы с окружающей средой (J_s, I_s) и вследствие действия в элементе объема источника энтропии мощностью (q,Q), обусловленного необратимыми процессами. Источник энтропии всегда положительно определен, поскольку энтропия может лишь возникать в необратимых процессах.