Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 24

При   изучении   тепловых   и   энергетических   свойств   макроскопических   систем,   состоящих   из большого  числа  частиц  и  находящихся  в  состоянии  статистического  равновесия  или  близком  к нему, техническая и статистическая термодинамика дополняют друг друга. 

7.2.  Функции распределения                                                                         

В  термодинамике рассматривается  усредненное движение,  так как  всем частицам  объема dV приписывается  одинаковая  скорость  перемещения.  В  действительности   же  движение   частиц  является беспорядочным,  они  постоянно  сталкиваются  друг  с  другом и  поэтому имеют  скорости, различные по  модулю  и  направлению.  С  помощью  статистических  методов  можно  определить закон распределения  частиц  по  скоростям,  который  оказывается вполне  определенным (несмотря  на хаотичность движения частиц).                                                                                   

Распределение   частиц   по    скоростям   определяется    функцией   распределения ,  показывающей  среднее  по времени  число   частиц данного   вида в    данном  элементе   объема,  которые   имеют  скорости, лежащие в заданном интервале.                                                                      

Практическое  значение  функции распределения  состоит  в том,  что любая  величина, явно зависящая  от  скорости  частиц  и, следовательно,  от  ,  представляет собой  некоторую среднюю характеристику газа.  Действительно, полное  число частиц  всех скоростей.  в элементе  объема определяется интегралом                                                                                 

                                ,                                                              (14.1)

с помощью которого можно вычислить среднюю скорость частиц в элементе объема                       

v = =/,                                                                                    

                                                                                               (14.2)                                                                                         

а следовательно, и среднюю кинетическую энергию частиц с одинаковой массой m

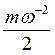 =              (14.3)                                         

среднюю плотность вещества                                                                     

 = m(14.4)                                                   

среднюю плотность электрического тока (для плазмы)                           

j = (14.5)                           

где   - скорость ионов;  Z_ie- заряд иона;   r- координата;  t - время. Таким образом, при известной функции распределения все макроскопические характеристики среды определяются однозначно. При этом следует учитывать, что для среды, имеющей в своем составе несколько видов частиц, функции распределения необходимо определять отдельно для каждого из этих видов.

Для рассмотрения многих теоретических и прикладных задач очень важным является распределение совокупности частиц, находящихся в тепловом равновесии.

Если большое число частиц находится в ограниченном пространстве в котором не действуют какие-либо дополнительные силы, и каждая из частиц взаимодействует с другими в течение продолжительного времени, то в системе установится равновесное состояние и соответствующее ему распределение частиц по скоростям. В этом состоянии число частиц, скорость которых при столкновениях увеличивается, будет равно числу частиц скорость которых в результате столкновений уменьшается. Выражение для  функции распределения частиц по скоростям в системе, находящейся в тепловом равновесии, было получено Дж. К. Максвеллом.

В равновесном стационарном состоянии число частиц с данными значениями скорости, несмотря на столкновения друг с другом, остается в системе неизменным. Следовательно, в этом случае можно принять что столкновения между частицами не влияют на вид функции распределения.