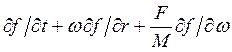Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 27

  =f_{ст                                                     (14.22)}

Это и есть кинетическое уравнение Больцмана, или кинетическое уравнение с правой частью.              

Известно,  что  столкновения  стремятся  перевести  систему  в  некоторое   квазиустойчивое  равновесное состояние. Поэтому интеграл столкновений приближенно можно представить в виде              

f_ст==     (14.23)                                                                

Здесь  и  f₀  -  начальная     установившаяся  функции распределения,  -  характерное время установления  функции  распределения,  по  порядку  величины  равное  времени   свободного  пробега частиц.                                                                                           

Решение   уравнения   Больцмана   представляет   немалые трудности.  При   современном  состоянии теории  функции  распределения    удалось   найти  только   для  некоторых   предельных  случаев.

Пусть,  например,  направленные  скорости  частиц  u много  меньше хаотических (тепловых) скоростей  т.е. u<<  В этом случае можно считать, что внешние поля на систему практически  не действуют и     решение этого уравнения имеет вид                                   

                            (14.24)

где    -  функция  распределения  частиц  по  скоростям  в  начальный  момент  времени; f₀ - максвелловская  функция  распределения.  Из  (14.24)   видно,  что   система  стремится   к  равновесному максвелловскому  состоянию  за время,  близкое  по  порядку  времени  между  соседними  соударениями частиц.

Если   же   длина   свободного   пробега  частиц   l  много   больше  характерного   размера  системы L(l>>L) , то это  случай бесстолкновительной  системы, для  которой справедливо  кинетическое уравнение без правой части (14.21). Случай, когда  l<<L ,  характерен для  сплошной среды,  в которой времена свободного пробега частиц   малы, и в системе достаточно быстро устанавливается максвелловское распределение.                                                                                         

 7.4.  Квантовая статистика                                                                                       

В классической механике состояние любой системы однозначно определяется координатами и им пульсами всех ее частиц, если для какого-то момента времени эти параметры заданы. В квантовой механике дело обстоит значительно сложнее, так как координата и импульс, энергия и время, а так- же другие пары динамических величин, характеризующих состояние любой микрочастицы, не могут одновременно иметь строго определенные значения.                                                                 

Эта ситуация называется принципом неопределенности Гейзенберга, смысл  которого  характеризуется соотношением  и 

где   h - постоянная Планка: p, x, E и -  меры  неопределенности импульса, координаты, энергии и времени соответственно. Следовательно, в квантовой механике определяется лишь вероятность нахождения системы в каком-то одном состоянии из числа многих возможных что отражает дискретный характер энергетических состояний системы.                                                                                                           

Пусть, например, в большой системе, состоящей из подсистем, осуществляется обмен различными формами энергии. В  этом случае каждая из подсистем может принимать свое, индивидуальное  значение  энергии Е_j и тогда  полная энергия системы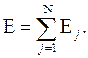

Однако из-за принципа   неопределенности  макросостояние  любой  подсистемы, а  следовательно,  и  всей  системы  в  целом в, каждый  момент  времени  не может  характеризоваться  каким-то   определенным  значением   энергии  Е.