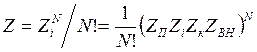Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 29

    (14.34)

Распределение  вероятностей,  как  следует  из  определения,  должно  быть при  этом равно  единице .

Пусть  взаимодействуют  друг  с  другом  две  системы, которые  находятся  в   тепловом  равновесии  и,  следовательно,  обладают  одинаковой  температурой.   Из  анализа  выражений  (14.25) и (14.26) видно, что у таких  систем одинаковы  значения параметра . Можно  показать, что  параметр  является  функцией  температуры  и  равен  =1/(kT). Это  дает  возможность   представить  распределение любых систем (молекул, атомов, ионов и др.) по энергетическим состояниям в виде                 

       (14.35)

Выражения (14.25) и (14.35) являются различными формами записи  к в а н т о в о г о канонического р а с п р е д е л е н и я Г и б 6 с а,  которое характеризует  распределение вероятностей различных состояний систем, находящихся в статистическом равновесии.                                 

Распределение Гиббса    позволяет  определять   среднее     значение   любого    физического   параметра, явно зависящего от   состояния  системы.  Так,  если  какой-то  параметр  при энергии  Е_m имеет значение Q_m                                 , то выражение для определения его среднего  значения  получит вид                            

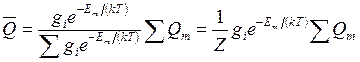
Для  систем  с  большим  числом  частиц  распределение  Гиббса  имеет  резкий  максимум  при некотором  значении  энергии.  Состояние,  отвечающее  этому  максимуму,  является   наиболее  вероятным, и  именно  оно  вносит  основной вклад  в среднее  значение любого параметра. Если  систему составляют  молекулы  идеального  газа,  то  распределение  Гиббса  переходит  в  распределение  Больцмана(14.20)  

   7.5. Определение термодинамических параметров  статистическими методами                                                                            

Статистическая термодинамика позволяет определить значения термодинамических параметров любой системы с использованием полученных зависимостей и статистических характеристик. Как  уже отмечалось, одной из Важнейших характеристик термодинамических систем является статистическая сумма  по состояниям Z, значения  которой зависят  исключительно от  молекулярных свойств системы,  а именно:  возможных энергетических  состояний, температуры    Т и  давления     р.  Это дает основание  использовать  статистическую   сумму  для   определения  значений   любых  термодинамических параметров. Свободная  энергия   F  является  функцией  состояния  системы.  Поэтому  статистическая сумма по состояниям может быть представлена в виде 

         (14.36)

Отсюда                                                                                            

                                                                         (14.37)

Это  выражение  является  основным  для  определения  термодинамических  параметров  статистическими  методами,  с помощью  которых, учитывая  известные связи  свободной энергии  с термодинамическими параметрами, можно найти:                                                                 уравнение состояния системы                                                                   

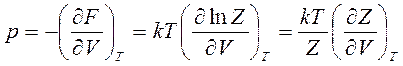(14.38)

энтропию                                                                                     

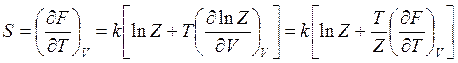      (14.39)

внутреннюю энергию                                                                           

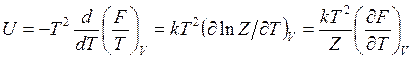                  (14.40)

энтальпию

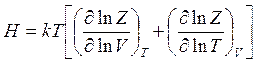(14.41)

теплоемкость при постоянном объеме                                                          

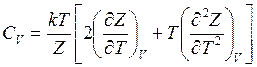            (14.42)

теплоемкость при постоянном давлении

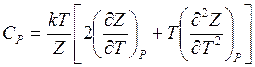    (14.43)

изобарно-изотермный потенциал

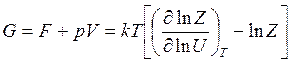                           (14.44)

Таким  образом,  при  известном  выражении  для  статистической  суммы Z любой  системы ее термодинамические параметры определяются выражениями (14.37) - (14.44) однозначно.