Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 35

Выражения для потоков J_i и сил Х_i  в каждом конкретном случае могут быть получены из анализа зависимости для скорости производства энтропии (см.  14.7).     

8.3.  Применение теории Онсагера к анализу процессов теплопроводности                                                                                                   

Рассмотрим  цилиндр  из  материала  с  изотропными свойствами,  в котором  вдоль направления оси х имеется градиент температур. Предположим, что задача одномерная, тогда направление теплового потока совпадет с градиентом температуры (рис. 14.2).                                                      

Выделим  элементарный  цилиндрический  объем  длиной dx с  единичной   площадью поперечного сечения. Согласно первому началу термодинамики, изменение внутренней энергии  элемента должно быть равно разности входящего и покидающего  элементарный объем  тепловых потоков  за единицу времени:

 (14.68)

где  u - удельная внутренняя энергия, Дж/кг; p - плотность, кг/м,                 q- тепловой поток, Дж/(м с); - время, с.                                                                                         

Имея в виду, что для данного случая, согласно второму началу термодинамики,                                  

du=Tds

запишем уравнение ( 14.68) в виде                                                                                

Так как 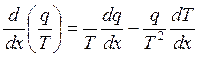 окончательно получим выражение для скорости возникновения энтропии.

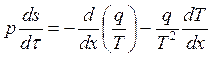 (14.69)

Первый член соответствует  потоку энтропии J_s=q/T, поступающему в элементарный объем извне, в то время как второй член связан с производством (скоростью возникновения) энтропии в объеме за счет необратимости процессов переноса теплоты.

Таким образом, скорость производства энтропии                                                     

                            (14.70) где  gradT=dT/dx.

Согласно уравнению (14.62), соотношение (14.70) можно представить в виде

 , 

где J_q=q; X_q=-gradT/T².

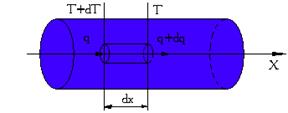Рис. 14.2. Теплопроводность неограниченного цилиндра

При таком определении потока и силы феноменологический закон  переноса теплоты примет вид                                                                                                

(14.71)

Если сопоставить уравнение (14,71) с законом Фурье  q=-gradT,                   , то феноменологический коэффициент L  можно выразить через теплопроводность в следующем виде:                                                         

Если принять в качестве выражения для производства энтропии уравнение (14.66), то в этом случае получим   следующее выражение для силы                                                                           

В случае стационарного процесса теплопроводности энтропия сохраняет постоянное значение в любой точке цилиндра, а суммарное производство энтропии равно нулю, т. е.

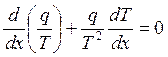 (14.72)

Однако  в  этом  случае  поток энтропии   не  остается постоянным  вследствие уменьшения температуры вдоль оси  . Соотношение (14.72]  свидетельствует лишь о том, что  поток энтропии,  покидающий элемент, равен ее производству в элементарном объеме за счет неравновесности процесса переноса теплоты.

  8.4. Применение теории Онсагера к  анализу  термоэлектрических эффектов                                                                                                

У.  Томсон  (Кельвин), применяя  законы термодинамики  равновесных процессов,  создал в  1854 г. теорию  термоэлектрических  явлений,  которая  приводит  к  результатам,   подтверждаемым  опытом.