Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 4

Следовательно, внутренняя энергия является термодинамическим параметром состояния системы, зависящим однозначно от основных параметров. Изменение основных параметров системы не зависит от пути перехода системы из одного состояния в другое, а определяется только ее начальным (1) и конечным (2) состоянием.

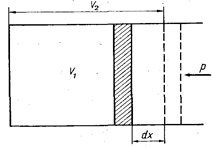
Рис. 2. Схема к определению работы расширения газа

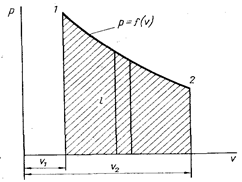
Рис.  3.   Графическое изображение процесса в координатах pv

Это положение справедливо и для внутренней энергии. Поэтому dU = U₂-U₁.

Внутренняя энергия изолированной системы не меняется при изменении ее параметров. Неизолированная система обменивается с окружающей средой теплотой и работой, что приводит к изменению внутренней энергии.

Работа газа осуществляется при изменении объема рабочего тела (рис. 2). Если газ под поршнем, имеющим площадь F, изменит объем от V₁ до V₂, то при этом он произведет работу против сил давления окружающей среды р. Элементарная работа dL, затрачиваемая для перемещения объема газа Fdx = dV, равна dL = р dV. Работа расширения газа в процессе

L=рdV  или l=рdv.                                                         (1.2)

Величина работы определяется зависимостью изменения рабочего тела при изменении его давления

L =f(p). Поэтому работа является функцией термодинамического процесса.

Обратимые термодинамические процессы часто изображают графически в системе координат pu (рис. 3). Точками 1 и 2 обозначены начальное и конечное состояние системы. Заштрихованная площадь, заключенная между кривой, осью абсцисс и двумя ординатами, будет равна энергии, полученной или затраченной рабочим телом в соответствии с уравнением (1.2). Кроме работы расширения, определяемой уравнением (1.2), возможны случаи, когда работа над телом совершается без изменения его объема. Это, например, вращение жидкости мешалкой, которую можно считать внешним источником работы l_v. Тогда в общем случае

l=рdv+ l_v.

Если же p =const и l_v. = 0, то

l = рv₁ – рv₂.                                                                             (1.3)

Количество теплоты, воспринятой рабочим телом от окружающей среды, пропорционально его массе М, теплоемкости с и изменению температуры тела dТ, т. е. 

dQ = Мс dТ.

Если температура системы меняется от T₁ до Т₂, то количество тепла, воспринятого или отданного системой:

Q=McdT или q=cdT                                              (1.4)

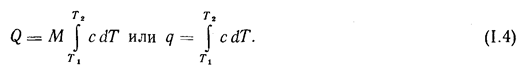
В этих выражениях теплоемкость не выносится за знак интеграла, ибо она является функцией температуры. Она зависит также от условий осуществления термодинамического процесса. Поэтому теплота не является функцией состояния системы. При всяком изменении состояния системы ее внутренняя энергия изменяется. Величину u = V/ М называют удельной внутренней энергией.

Для системы, состоящей из нескольких тел, U= U_i т. е. внутренняя энергия системы тел обладает свойством аддитивностн.

1.3. Первый закон термодинамики. Энтальпия

Первый закон термодинамики является частным случаем закона сохранения энергии применительно к термодинамическим системам. В технической термодинамике изучается обмен энергией системы с окружающей средой в форме теплоты и работы.

При одновременном тепловом и механическом взаимодействиях системы со средой изменение внутренней энергии будет зависеть как от количества подведенной теплоты, так и от произведенной системой работы, т. е.

где Du — изменение внутренней энергии термодинамической системы.

В соответствии с последним уравнением первый закон термодинамики можно сформулировать следующим образом. Теплота, подведенная к термодинамической системе, идет на изменение  внутренней энергии системы и на совершение ею внешней работы.

В дифференциальной форме уравнение (1.5) можно записать так:

В этом уравнении dи является полным дифференциалом в отличие от dq и dl, которые определяют только бесконечно малые количества теплоты и работы. Значения q и l не являются параметрами состояния, так как они зависят от характера процесса перехода системы из одного состояния в другое.