Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 6

Работа, производимая двигателем, строго равна количеству теплоты, воспринятой рабочим телом от внешнего источника. Это соответствует первому закону термодинамики. Если бы это равенство не соблюдалось, то можно было бы сделать предположение о том, что возможно построить двигатель без подвода теплоты извне. Это равносильно осуществлению так называемого вечного двигателя первого рода. Вследствие этого второй закон термодинамики формулируют так: вечный двигатель первого рода невозможен.

Первый закон термодинамики определяет процессы превращения энергии с количественной стороны, а второй закон характеризует их качественную сторону.

Часто второй закон термодинамики формулируют так: любой самопроизвольный процесс является необратимым. Таким необратимым процессом является переход теплоты от тела с более высокой температурой к телу с меньшей температурой.

В 1850 г. Клаузиус привел иную формулировку второго закона: теплота не может самопроизвольно переходить от холодного тела к более нагретому. Чтобы осуществить этот процесс, нужно совершить работу.

Работа может совершаться только системой, выведенной из состояния равновесия. Для теплового двигателя это соответствует наличию двух источников теплоты, имеющих разную температуру. Наличие двух источников теплоты предопределяет тем самым неполный переход тепловой энергии в периодически повторяющемся цикле в работу. Часть тепловой энергии горячего источника должна быть передана холодному источнику. Тепловую машину, имеющую один источник теплоты, В. Ф. Оствальд назвал вечным двигателем второго рода. Выражение

называют основным уравнением термодинамики, а входящую в него величину dq/T — приведенной теплотой на бесконечно малом участке термодинамического цикла.

Приведенная теплота обладает весьма важным свойством: ее изменение в каком-либо обратимом процессе определяется лишь начальным и конечным состоянием рабочего тела. В самом деле, сопоставляя уравнение (1.8), записанное для элементарного обратимого цикла, с выражением (1.8а), находим:

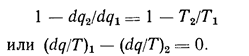
Поскольку подведенную теплоту принято считать положительной, а отведенную — отрицательной, то последнее соотношение можно переписать в виде

Рассматривая обратимый цикл как совокупность бесконечно большого числа элементарных циклов, получим:

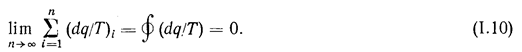
Это уравнение представляет собой математическую запись второго закона термодинамики для обратимых циклов.

Таким образом, приведенная теплота на бесконечно малом участке термодинамического цикла является, подобно внутренней энергии, параметром состояния системы. Она позволяет однозначно выделять обратимые процессы из всего множества возможных. По этой причине dq/T  обозначают ds, где s — новый параметр состояния, называемый энтропией. Используя понятие энтропии, можно записать:

т. е. в обратимом цикле изменение энтропии равно нулю (Ds= 0). Знак перед численным значением энтропии будет определяться только знаком теплоты, ибо абсолютная температура — величина положительная. Поэтому в термодинамических процессах, сопровождающихся подводом теплоты, изменение энтропии системы будет положительным, а при отводе теплоты — отрицательным.

Термодинамические процессы можно изображать графически в системе координат Тs. Зная вид функции, описывающей зависимость изменения энтропии от температуры, интегрированием ее можно определить количество теплоты, превращенной в работу, т. е. 

Круговые процессы изображают в системе координат Тs замкнутой кривой (рис. 4). Площадь, ограниченная верхней кривой, крайними ординатами и осью абсцисс, соответствует количеству теплоты, подведенному к системе. Площадь под нижней кривой эквивалентна теплоте, отведенной от системы. Площадь между кривыми представляет собой превращающуюся в работу разность количеств теплоты, подведенного к системе и отведенного от нее, т. е. q₁ –q₂= l. Уравнение (1.9) можно записать так: Tds= du+ dl =di+u dp. Эти уравнения объединяют первый и второй законы термодинамики. В соответствии с ними можно записать. что