Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 34

Так  например,  жидкость  течет  сверху  вниз,  теплота   самопроизвольно  переходит   от нагретого тела к холодному, движение газа направлено в сторону убывания давления и  т. п.,  но никто и никогдане   наблюдал   обратного.   Таким   образом,  направление   переноса  субстанции   противоположно положительному градиенту соответствующего термодинамического потенциала.                           

Конкретные  выражения  для  потоков J_i и  сил  Х_i Онсагер  предложил определять  из анализа выражения для скорости возникновения энтропии в неравновесных процессах

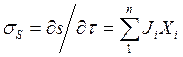(14.62)

полученного  в  результате  анализа  поведения  развивающейся  адиабатно   иэолированной  термодинамической  системы.  Это  выражение  можно  также  получить  из  следующих  соображений* .  Элементарное количество  внешних   воздействий  в   любом  неравновесном   процессе  может   быть  представлено в следующем виде:                                                                      

(14.63)

где  dQ_i=-dL_i- элементарное количество внешних воздействий; dL_i- элементарная работа данного рода; P_i^e- внешний термодинамический потенциал; x_i - координата состояния.

Связь  между внешним P_i^e и внутренним  Р_i  потенциалами следует из соотношения P_i^e= Р_i+d Р_i

Таким образом, уравнение (14.63) принимает вид

 (14.64)

В  случае  протекания  равновесных  процессов  (при  равенстве  внешнего и  внутреннего потенциала) второй член в  (14.64) стремится  к нулю  и выражение  для количества  внешних воздействийравное и обратное по знаку элементарной работе. записывается в виде

Дополнительное слагаемое dР_idx_i, появляющееся в (14.64), представляет собой потери, связанные  с  неравномерностью.  Опыт  показывает,  что  преобразование  любых  форм  движения материи, связанное с необратимыми потерями, всегда происходит в одном  направлении, т.  е. в  конечном счете все  формы  движения  преобразуются  в  теплоту диссипации,  что, в  свою очередь,  согласно второмузакону термодинамики, приводит к росту энтропии термодинамической системы:

(14.65)

Из соотношения (14.65) следует, что                                                           

Из последнего равенства нетрудно получить выражение для скорости возникновения энтропии в  единице объема в виде                                                                              

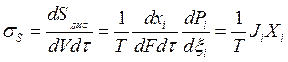(14.66)

где  dV=dFd_i -  элементарный  объем; F-  площадь  поперечного  сечения; _i -  координата, совпадающая  с  направлением  потока; J_i=dx_i/(dFd)- поток  величины ,  Х_i=dP/d_i - движущая сила в направлении оси i .                                                                           

Если   термодинамическая   система  обладает связанными   степенями  свободы,   то  суммарная скорость возникновения энтропии определяется выражением                                            

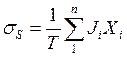(14.67)      практически совпадающим с выражением (14.62), полученным Л. Онсагером.                                             

Следует заметить, что уравнение (14.67) предоставляет некоторую свободу выбора потоков  J_i и сил Х_i . Однако, несмотря на это, феноменологические коэффициенты в уравнении (14.58) будут подчиняться соотношениям взаимности (14.60) Онсагера.                                                               

Ниже приведены некоторые наиболее часто используемые  выражения для  потоков     и обобщенных сил Х_i .