Уравнение (1.6) можно записать так: dq =du + d (рu) -udp, илиdq =d(u + рu)- udp.
Величина (u + рu), состоящая из параметров состояния, сама является параметром состояния. Ее называют энтальпией и обозначают i, т. е. i = u + рu. Обычно отсчет энтальпии производят от 0° С. Она обладает свойством аддитивности. Уравнение первого закона термодинамики примет вид:
Если процесс осуществляется при p = const, то dq = dh. Поэтому при p = const вся теплота в процессе, в котором нет изменения давления, расходуется на изменение энтальпии. Из уравнения (1.7) можно получить, что при u = const
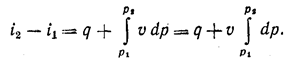
Очевидно, при постоянном объеме изменение энтальпии системы больше теплоты на величину полезной работы.
В начале XIX в. в промышленности получили широкое распространение паровые машины. Перед конструкторами, стремящимися разработать наиболее экономичные машины, встал вопрос о том, насколько полно в этих машинах сообщаемую пару теплоту можно превратить в работу.
Первый закон термодинамики устанавливает возможность взаимного перехода теплоты в работу и работы в теплоту, но не определяет условий их превращения, не указывает возможные направления протекания этих процессов.
В 1824 г. французский инженер Сади Карно опубликовал труд «Размышление о движущей силе огня и о машинах, способных развивать эту силу», в котором использовал теорию теплорода, а паровую машину уподобил водяной турбине. Известно, что мощность мельницы будет тем выше, чем больше будет разность уровней воды в верхнем и нижнем водоемах. Используя эту аналогию, Сади Карно показал, что для совершения тепловой машиной работы необходимы два источника теплоты с различными температурами. При этом количество теплоты Q1, переданной горячим источником (нагревателем), никогда не может быть полностью превращено в работу, так как часть этого количества теплоты Q2 должна быть отведена в холодильник. Было также показано, что движущая сила в паровых машинах возникает не в результате расхода теплорода, а вследствие его перехода от горячего тела к холодному. В соответствии с теорией Карно количество теплоты, которое возможно превратить в работу, определяется разностью подводимого к машине и отводимого от нее количеств теплоты, т. е. Q1-Q2.
В паровой машине осуществляется круговой цикл. В цилиндрах машины пар расширяется от начального давления р1 до конечного р2. При этом производится работа расширения Lp. Для повторного совершения работы расширения нужно вернуть систему в исходное состояние, т. е. сжать пар, затратив энергию Lc. Чередующиеся процессы расширения и сжатия образуют цикл. Процессы расширения и сжатия рабочего тела, изображаемые с помощью pu - диаграммы, должны быть разными. В этом случае разными будут и площади под кривыми процесса. Если Lp > Lc , то машина будет совершать за цикл полезную работу Lц.
Дифференциальное уравнение первого
закона термодинамики для рабочего тела массой М имеет вид dQ = dU + dL. Интегрируя его, для цикла получим 
dQ= dU+ dL
Внутренняя энергия системы является функцией состояния. При возвращении
рабочего тела в исходное состояние она приобретает также исходную величину. Поэтому
dU = 0. ТогдаdQ= dL
. ИлиQц = Lц =Lр -
Lс.
Следовательно, работа цикла равна количеству теплоты, подведенной извне к рабочему телу. Величина Qц = Q1- Q2 . Поэтому коэффициент полезного действия машины, представляющий отношение работы к подведенной теплоте:
Воспользовавшись соотношением (1.4), можно показать, что к. п. д. обратимого цикла не зависит от природы рабочего тела и в этом случае однозначно выражается через абсолютные температуры горячего и холодного источников теплоты, т е
Очевидно, h < 1. Следовательно, теплоту, подводимую к рабочему телу, нельзя полностью превратить в работу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.