![]()
Видно, что движение газа без теплообмена и технической работы — разгон газа, т. е. увеличение его скорости обязательно сопровождается уменьшением его энтальпии и понижением температуры.
Уравнение Д. Бернулли при изоэнтропическом движении имеет вид:
![]()
Следовательно, скорость газа увеличивается только при понижении давления. Наоборот, торможение газа, уменьшение его скорости сопровождаются увеличением давления потока газа. Каналы, в которых осуществляют разгон газа, называют соплами. В соплах по ходу газа скорость возрастает, а давление, энтальпия и температура понижаются.
Каналы, в которых происходит торможение газа — уменьшение его скорости, называют диффузорами. В диффузорах по направлению движения потока скорость уменьшается, а давление, энтальпия и температура растут. При изоэнтропном течении
i + 0,5w2 = const.
Если скорость будет равна нулю, то вся кинетическая энергия потока преобразуется в энтальпию, что приведет к повышению энтальпии газа. Эту энтальпию называют энтальпией торможения и обозначают i*. Такую энтальпию имеет газ до начала своего движения, а также после полной остановки движущегося потока.
При движении идеального газа постоянной остается и другая сумма, т. е.

Здесь 0,5w2/cр, имеет размерность температуры. Эту величину называют динамическим повышением температуры газа при торможении, а Т* — температурой торможения. Если поток несжимаем, то u = 1/r = const. Поэтому
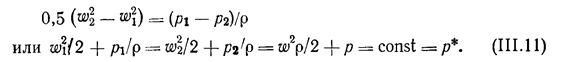
Здесь w2r /2 — динамическое давление, р — статическое давление, а р* — давление торможения.
Для газа давление торможения вычислить трудно, ибо плотность газа является функцией давления. Так как T = (рu)/ R. = р/r (ср - сu), то уравнение (111.10) можно записать и так:
![]()
где r* = r (р*/р) 1/ k — плотность торможения.
Уравнение (111.12) называют уравнением Д. Бернулли для потока сжимаемого газа.
При продувке стали в конверторах, подаче природного газа или мазута в доменные, мартеновские и нагревательные печи используют сопла различной формы, которые позволяют энтальпию потока превратить в кинетическую энергию и повысить скорость его движения. Сопла представляют собой короткие насадки, в которых движущийся поток можно считать изоэнтропическим. Расчетом определяют поперечное сечение сопла, скорость и расход газа на выходе из него, а также некоторые другие характеристики.
В соответствии с уравнением (111.8) скорость потока, м/с, на выходе из сопла
![]()
Если газ вытекает из большего резервуара,w1 = 0, а энтальпия равна энтальпии торможения i*. Поэтому скорость истечения газа из резервуара
![]()
Здесь haд — адиабатный тепловой перепад энтальпии. Далее принято, что
![]()
Для идеального газа при адиабатном процессе u1 – u2 = l. Воспользовавшись уравнением (11.14), получим, что
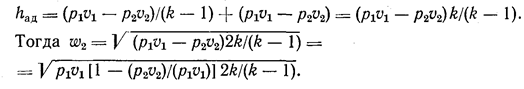
Скорости истечения удобнее выразить через давление потока на входе и выходе из сопла. Для этого отношение р2/р1 обозначим b и выразим отношение удельных объемов через отношение давлений. Так как
![]()
Поэтому теоретическая скорость истечения газа, т. е. Скорость без учета потерь энергии на трение
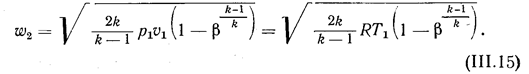
Секундный расход газа, кг/с, можно определить с помощью уравнения неразрывности Gм = (f w)/u2. Здесь f — площадь сопла, а u2 — удельный объем газа при выходе из сопла.
Из уравнения адиабаты р1u k1 = р2u k2 получим, что u2 =u1 (р1/ р2)1/ k.
Подставив последнее соотношение в выражение для расхода газа, получим:
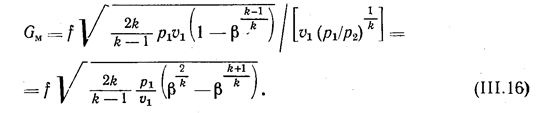
Видно, что величина Gм зависит от площади сопла, свойств и начальных параметров газа (k, р1, u1), а также давления окружающей среды р2 (b). Видно, что при некоторых значениях b расход газа достигает максимума. То значение b, при котором расход газа достигает максимума, называют критическим bкр, а давление, ему соответствующее, — критическим давлением ркр. После дифференцирования выражения в круглых скобках уравнения (111.16) и приравнивания производной нулю можно найти, что
![]()
Тогда ркр = bкр р1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.