Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 26

=                                                        (14. 15)

С р е д н я я   скорость частиц ансамбля определяется соотношением                        

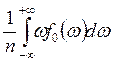==                                                     (14.16)

Так как  ==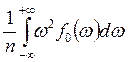то среднеквадратическая   скорость                      

=(14.17)

Сравнение полученных выражений показывает, что относительные значения трех характерных скоростей близки между собой:                                                                  

=1:1,13:1,22

Максвеловское распределение частиц по скоростям справедливо для случая, когда полная энергия частиц совпадает с их кинетической энергией поступательного движения.                  

Однако на практике на  ансамбль частиц  часто действуют  также внешние  силовые потенциальные  поля.  В  этом  случае  полная  энергия  частиц E=E_k+E_пот, где E_k=   - кинетическая энергия  поступательного  движения;  Е   -  потенциальная  энергия  во  внешнем  силовом  поле, зависящая от координат, С учетом этих обстоятельств выражение (14.14) получит вид                  

f=                        (14.18)

Распределение  частиц,  удовлетворяющее этому  выражению и  называемое     р а с п р е д е л е н и  е м   М а к с в е л л а - Б о л ь ц  м а н а,  можно рассматривать  в качестве  произведения вероятностей двух независимых событий: вероятности данного значения скорости                                

                               = (14.19)                                                                

и вероятности, отвечающей данному значение потенциальной энергии,                                   

=                                        (14.20)

где   n₀ - плотность частиц в плоскости  r =0.                                                         

Выражение (14.19) описывает распределение частиц и пространстве скоростей и являются уже известным  распределением  Максвелла. Выражение  (14.20), описывающее  распределение частиц в силовом потенциальном поле, называется- распределением Больцмана.                                   

Одним из  наиболее часто  встречающихся случаев  больцманского распределения является распределение частиц в поле сил тяготения E_пот=mgh. При этом n=. Полученное выражение называется барометрической формулой.                                                     

   7.3.  Кинетическое уравнение Больцмана                                                              

Зависимость  изменения  функции  распределения   от  времени,   координат  и   скорости  определяется кинетическим уравнением. Так  как  в  реальных  системах  взаимодействия  между. частицами  очень многообразны,  то для, описания  таких  систем  обычно   используются  приближенные   методы,  среди   которых  наибольшее распространение  получило  кинетическое  уравнение  Больцмана.  Оно  описывает   поведение  функции, распределения   в   приближении   дискретного  парного   взаимодействия  между   частицами  системы.

В этом случае   =f_ст , где  f_cт - так называемый        и н т е г р а л       с т о л к н о в е н и й, который учитывает  изменение  функции  распределения  (числа  частиц)   в  результате   парных  соударений . При  отсутствии  столкновений  движение  частиц  и   изменение  функции   распределения  определяются только внешними полями и значениями f_cт =0. Тогда   

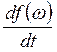==0

Учитывая, что =F/M и   =, получаем                                                    

                                                                                              (14.21)

где  F- сила, действующая на частицу массой М; r- координата;   t - время                          

Это бесстолкновительное кинетическое  уравнение, или,  как часто называют, кинетическое уравнение без правой части. Динамика всей системы в этом случае определяется силой F

Если  же  столкновения  между  частицами  существенны,  то   правая  часть   кинетического  уравнения   должна  отражать   скорость  изменения   функции  распределения,   вызываемую  столкновениями, поэтому