В аэродинамике его называют уравнением неразрывности. В качестве открытой термодинамической системы рассмотрим систему, представленную схематически на рис. 10. Поток газа поступает под давлением р1 в теплотехнический аппарат со скоростью w1. Параметры газа T1 и u1, площадь сечения канала f. Ось входного патрубка расположена на некоторой высоте H1 от условного уровня отсчета. В аппарате поток получает от внешнего источника теплоту и совершает над внешним объектом техническую работу lтех, а затем удаляется через выхлопной патрубок, имея параметры р2 Т2 и u2 со скоростью w2. Сечение этого патрубка f2, а его ось расположена на высоте H2 от того же уровня отсчета.
В соответствии с первым законом термодинамики q = Du + l Для рассматриваемого случая работа изменения объема
где lп - суммарная работа потока против внешних сил или работа проталкивания; lт - техническая работа, например по приведению в движение ротора турбины; lk - работа, затраченная на изменение кинетической энергии потока в сечениях 2 и 1; lпот - работа, затраченная на изменение потенциальной энергии потока в аппарате.
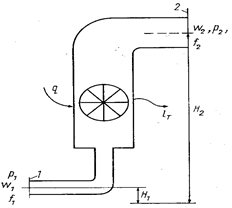
Рис. 10. Схема открытой термодинамической системы
Работа проталкивания lп = p2u2 - p1u1 где p2u2 и p1u1 - работы выхода 1 кг газа из аппарата и подачи его в аппарат соответственно. Величина изменения кинетической энергии 1 кг газа lк = 0,5 (w22 - w21).
Потенциальная энергия 1 кг газа равна gН, а величина работы на ее изменение в аппарате lпот = g (H2 – H1). Поэтому уравнение первого закона термодинамики для движущегося потока приобретает такой вид:
Так как u + pu= I, то уравнение первого закона термодинамики для потока примет вид:
В соответствии с уравнением (1.7) q=i2 - i1
- 
u dp. Интеграл
этого выражения называют располагаемой работой lр,
он характеризует часть работы изменения объема рабочего тела, которая может
быть полезно использована на совершение технической работы и на изменение
энергии потока:
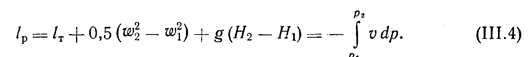
Знак располагаемой работы определяется знаком величины изменения давления. Для процесса расширения газа dp < 0, а величина интеграла будет положительной. Поэтому положительной будет располагаемая работа.
Располагаемая работа отличается от работы расширения газа, совершаемой в закрытой системе. В открытой системе работа затрачивается не только на сжатие или расширение газа, но также и на изменение его кинетической энергии.
Уравнение первого закона термодинамики для 1 кг стационарного потока будет иметь вид:
di = dq - dlр. (111.5)
Уравнение (111.3) при lт = 0 можно записать иначе:
В этом уравнении скорость газа связана с величинами термической природы. В него не вошли ни плотность, ни давление. Поэтому его называют уравнением энергии потока в термической форме. Уравнение не позволяет установить связь между изменениями скорости потока, определяющей его кинетическую энергию, и давления, от которого зависит величина потенциальной энергии. Поэтому часто уравнению энергии придают иную форму. Следует отметить, что наличие потерь энергии на преодоление трения газа о стенки канала не изменит смысл уравнения (111.3). В этом случае потерянная на трение кинетическая энергия lтр перейдет в теплоту, и общая энергия потока не изменится, ибо при адиабатных условиях работа трения перейдет в теплоту, расходуемую на повышение энтальпии газа. Для изотермических условий
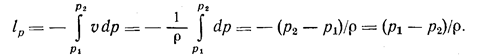
Тогда уравнение баланса механической энергии для движущегося потока примет вид (p1 – p2)/r =0,5 (w22 - w21)+ lт +lтр + g (H2 – H1) или
Форма записи уравнения энергии может меняться, физический смысл его — закон сохранения энергии. Обобщенное уравнение (111.7) полу-чено в 1738 г. Д. Бернулли.
Если при движении газа по каналу нет потерь энергии на трение и теплообмена со средой, то изменение энтропии потока будет равно нулю. Поэтому адиабатное движение газа без трения о стенки канала называют изоэнтропным. В этом случае, помимо уравнений энергии движущегося потока, можно пользоваться уравнениями связи между параметрами р, u, r и T. Если Н1 = Н2, то можно записать, что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.