Обычно такое состояние называют с о с т о я н и е м статистического р а в н о в е с и я.
При этих условиях в соответствии с теорией вероятности
![]() =
= ![]() (14.6)
(14.6)
![]()
где
![]() и
и ![]() - число
частиц со скоростями
- число
частиц со скоростями ![]() и
и ![]() до столкновения друг с другом;
до столкновения друг с другом; ![]() и
и ![]() - число
частиц со скоростями
- число
частиц со скоростями ![]() и
и ![]() после
столкновения. Если в качестве аргумента функции распределения взять квадрат
скорости, то выражение (14.6) получит вид
после
столкновения. Если в качестве аргумента функции распределения взять квадрат
скорости, то выражение (14.6) получит вид
![]() =
=![]() (14.7)
(14.7)
K процессу столкновения этих частиц применим закон сохранения энергии. В этом случае.
![]() +
+![]() =
=![]() +
+![]() (14.8)
(14.8)
С учетом выражений (14.7) и (14.8) имеем
![]() =
=![]()
После дифференцирования по ![]() и
и ![]() получим
получим
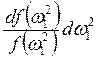 =
=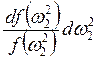 (14.9)
(14.9)
Скорости ![]() и
и ![]() были выбраны произвольно, в связи, с чем
можно сделать выводы о постоянстве выражения (14.9), т.
е.
были выбраны произвольно, в связи, с чем
можно сделать выводы о постоянстве выражения (14.9), т.
е.
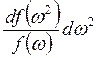 = -
= - ![]() (14.10)
(14.10)
или после интегрирования
![]() =
= ![]() (14.11)
(14.11)
Постоянную интегрирования А можно найти с помощью выражений (14.1) н (14.11), записанных вдоль одной из координатных осей, например х:
n
=![]()
Так как
![]() =
=![]()
то
A=![]() .
Если при том учесть три степени свободы,
то
.
Если при том учесть три степени свободы,
то
A=![]() (14.12)
(14.12)
Значение ![]() можно найти, если
применить уравнение, определяющее давление газа на стенки сосуда,
в который он заключен. Так как pV=NkT,
то p=nkT , где n=N/V . С другой стороны, давление р можно
подсчитать в виде интеграла произведения числа частиц ударяющихся о
стенку, на значение импульса, передаваемого при этих столкновениях в
единицу
времени:
можно найти, если
применить уравнение, определяющее давление газа на стенки сосуда,
в который он заключен. Так как pV=NkT,
то p=nkT , где n=N/V . С другой стороны, давление р можно
подсчитать в виде интеграла произведения числа частиц ударяющихся о
стенку, на значение импульса, передаваемого при этих столкновениях в
единицу
времени:
 p=
p=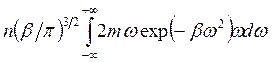
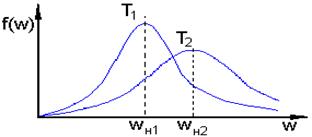
Рис. 14.1. Изменение максвеловской функции распределения по скоростям при различных температурах (Т1 < Т2 )
![]() =
=![]() (14.13)
(14.13)
С учетом полученных выражений равновесная максвелловская функция распределения частиц по скоростям принимает вид
![]() =
=![]() (14.14)
(14.14)
График (рис. 14.1) показывает, что при некоторых
значениях скорости ![]() и
и ![]() функции
распределения частиц по скоростям при разных температурах имеют свои максимумы.
Эта скорость называется наивероятнейшей, так как частицы со скоростью, близкой
к
функции
распределения частиц по скоростям при разных температурах имеют свои максимумы.
Эта скорость называется наивероятнейшей, так как частицы со скоростью, близкой
к ![]() чаще всего встречаются в массе частиц. При
этом следует заметить, что число частиц с очень большими и очень малыми
скоростями оказывается сравнительно небольшим, но они тем не менее всегда
имеются в любой системе. Для определения наивероятнейшей скорости
чаще всего встречаются в массе частиц. При
этом следует заметить, что число частиц с очень большими и очень малыми
скоростями оказывается сравнительно небольшим, но они тем не менее всегда
имеются в любой системе. Для определения наивероятнейшей скорости ![]() необходимо приравнять нулю производную
от
необходимо приравнять нулю производную
от ![]() ,
т.е.
,
т.е.
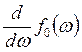 =
=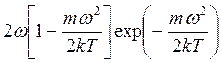 =0
=0
откуда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.