Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 30

В  предыдущем  параграфе  было  показано,  что  статистическая  сумма  по  состояниям  любой системы Z=Z_nZ_вн ,при этом статистическая сумма по состояниям энергиипоступательного движения  Z_n определяется  выражением  (14.28),  а  внутренней  энергии  Z_вн выражениями  (14.29), (14.30), (14.33) при  этом  статистическая  сумма по  состояниям энергии  поступательного движения. Поэтому  для получения  расчетных выражений  формулу (14.37)  свободной энергии следует записать в виде                                                                         

 (14.45)

или                                                                                             

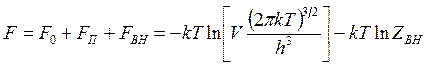  (14.46)

где  слагаемое   соответствует  поступательному движению,  а слагаемое   -  энергии  внутренних  степеней свободы  атомов или  молекул. Тогда  [см; (14.46) и (14.38) - (14.44) ] выражения для основных термодинамических  параметров примут вид:           уравнение состояния                                                                        

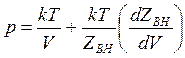( 14.47)

внутренняя энергия                                                                        

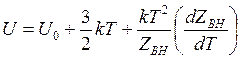(14.48)

энтальпия                                                                                

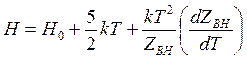 (14.49)

энтропия                                                                                 

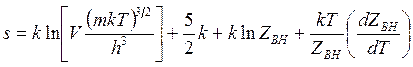             (14.50)

теплоемкость при постоянном объеме                                                       

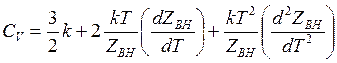(14.51)

теплоемкость при постоянном давлении                                                     

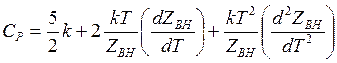 (14.52)

изобарно-изотермный потенциал                                                            

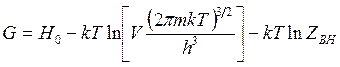(14.53)

Определяя  термодинамические  параметры  статистическими   методами,  следует   помнить,  что для одноатомных газов  Z_BH=g₀, но для двухатомных молекул выражение Z_BH гораздо  сложнее (см.соотношения (14.33) ) . 

8. Основы термодинамики необратимых процессов

Термодинамика необратимых процессов как раздел теоретической физики возникла в результате дальнейшего развития и обобщения положений классической термодинамики. Начало теории было положено в работах Онзагера [1], где была сформулирована линейная феноменологическая термодинамика необратимых процессов. Краткое, но содержащее все необходимые сведения, изложение физических основ феноменологической теории содержится в монографии Гурова [14]. При всей ее краткости она дает ясное физическое понимание основ теории.

Важным этапом развития термодинамики необратимых процессов явились поиски вариационной формулировки феноменологической теории. Для линейной термодинамики первые вариационные принципы были сформулированы в работах Онзагера, Пригожина и др [1, 4, 8, 9, 11]. В целом к настоящему времени линейная термодинамика необратимых процессов достигла своего логического завершения, получив строгое статистическое обоснование. Эти вопросы изложены в фундаментальной монографии Зубарева [16]. Дальнейшее развитие теории связано с проблемой построения термодинамики нелинейных процессов, рассматривающей системы, далекие от состояния термодинамического равновесия.

8.1. Общие положения термодинамики необратимых процессов

Классическая термодинамика устанавливает связи экстенсивных параметров системы — энтропии S, внутренней энергии U, объема V, массы k-гo компонента т_kв n-компонентной системе — и интенсивных величин — температуры Т, давления р, химического потенциала k-гo компонента m_k — в форме соотношения Гиббса:

 (1.1)

Его обобщение на случай неравновесных систем достигается на основе принципа локального равновесия. Последний постулирует сохранение условий равновесия в элементарных объемах системы при переходе ее во всем масштабе от равновесного состояния к неравновесному. По существу, предполагается справедливость соотношения Гиббса в локальной форме:

          (1.1а)

а вместе с ним и всех соотношений и величин классической термодинамики для неравновесных систем. Здесь d_i — оператор полной производной по времени t,